如图,在中,,的平分线交于点,点在上,以为直径的经过点.
(1)求证:①是的切线;
②;
(2)若点是劣弧的中点,且,试求阴影部分的面积.

如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长。小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题: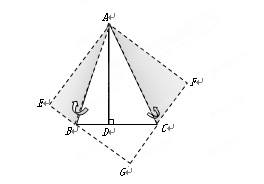
(1)AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,证明四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,留在墙上的影高为2米,求旗杆的高度.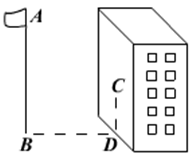
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,
求证:(1) ;(2)
;(2)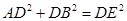 .
.
将分别标有数字1,2,3 的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?恰好是32的概率是多少.
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?