如图,二次函数的图象与轴交于点和点,与轴交于点,以为边在轴上方作正方形,点是轴上一动点,连接,过点作的垂线与轴交于点.
(1)求该抛物线的函数关系表达式;
(2)当点在线段(点不与、重合)上运动至何处时,线段的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点,连接、.请问:的面积是否存在最大值?若存在,求出此时点的坐标;若不存在,请说明理由.

如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: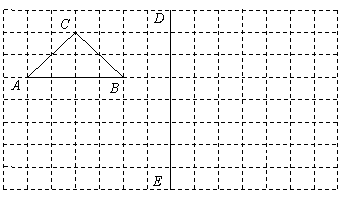
(1)画出△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1 ;
(2)在直线DE上标出一个点Q,使QA+QC的值最小.
进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:
如图所示,有两个长度相等的滑梯,左边滑梯BC的高AC与右边滑梯EF水平方向的长度DF相等,两滑梯倾斜角∠ABC和∠DFE有什么关系?并说明理由。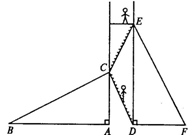
如图,在△ABC和△DCB中,AC与BD相交于点O.AB=DC,AC=BD.求证:OB=OC.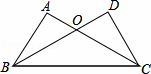
如图∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.