如图,在等边中,,动点从点出发以的速度沿匀速运动.动点同时从点出发以同样的速度沿的延长线方向匀速运动,当点到达点时,点、同时停止运动.设运动时间为.过点作于,连接交边于.以、为边作平行四边形.
(1)当为何值时,为直角三角形;
(2)是否存在某一时刻,使点在的平分线上?若存在,求出的值,若不存在,请说明理由;
(3)求的长;
(4)取线段的中点,连接,将沿直线翻折,得△,连接,当为何值时,的值最小?并求出最小值.

解下列分式方程:(1)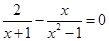 ;(2)
;(2)
如图,把一个等腰直角三角板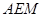 放置于矩形
放置于矩形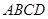 上,
上,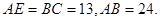 三角板的一个
三角板的一个 角的顶点放在
角的顶点放在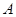 处, 且直角边
处, 且直角边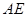 在矩形内部绕点
在矩形内部绕点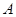 旋转,在旋转过程中
旋转,在旋转过程中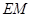 与
与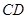 交于点
交于点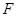 .
.
(1)如图1,试问线段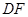 与
与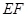 的有何数量关系?并说明理由;
的有何数量关系?并说明理由;
(2)如图1,是否存在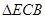 为等腰三角形,若存在,求出
为等腰三角形,若存在,求出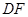 的长,若不存在,说明理由.
的长,若不存在,说明理由.
继续以下探索:
(3)如图2,以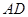 为边在矩形内部作正方形
为边在矩形内部作正方形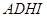 ,直角边
,直角边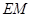 所在的直线交
所在的直线交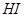 于
于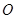 ,交
,交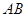 于
于 .设
.设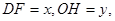 写出
写出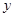 关于
关于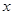 的函数关系式.
的函数关系式.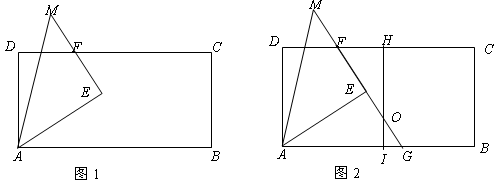
抛物线 交
交 轴于
轴于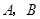 两点,交
两点,交 轴于点
轴于点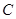 ,对称轴为直线
,对称轴为直线 。且A、C两点的坐标分别为
。且A、C两点的坐标分别为 ,
,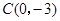 .
.
(1)求抛物线 的解析式;
的解析式;
(2)在对称轴上是否存在一个点 ,使
,使 的周长最小.若存在,请求出点
的周长最小.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
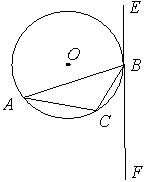
已知:△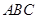 内接于⊙
内接于⊙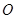 ,过点
,过点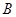 作直线
作直线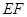 ,
,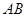 为非直径的弦,且
为非直径的弦,且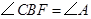 。
。
(1)求证: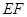 是⊙
是⊙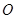 的切线;
的切线;
(2)若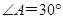 ,
,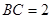 ,连结
,连结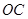 并延长交
并延长交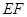 于点
于点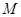 ,求由弧
,求由弧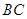 、线段
、线段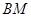 和
和 所围成的图形的面积.
所围成的图形的面积.
如图,等边三角形ABC中,D是AB边上的动点,以CD为一边,向上作等边三角形EDC,连结AE.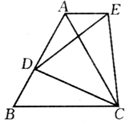
求证:(1)△ACE≌△BCD;
(2)AE∥BC.