小强的爸爸准备驾车外出．启动汽车时，车载报警系统显示正前方有障碍物，此时在眼睛点 处测得汽车前端 的俯角为 ，且 ，若直线 与地面 相交于点 ，点 到地面 的垂线段 的长度为1.6米，假设眼睛 处的水平线 与地面 平行．
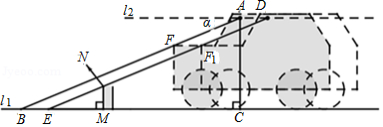
（1）求 的长度；
（2）假如障碍物上的点 正好位于线段 的中点位置（障碍物的横截面为长方形，且线段 为此长方形前端的边）， ，若小强的爸爸将汽车沿直线 后退0.6米，通过汽车的前端 点恰好看见障碍物的顶部 点（点 为点 的对应点，点 为点 的对应点），求障碍物的高度．
先化简再求值：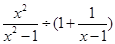
，其中
．
如图，在直角坐标系中有一直角三角形AOB，O为坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点O逆时针旋转900，得到△DOC。抛物线y=ax2+bx+c经过点A、B、C。
（1）求抛物线的解析式；
（2）若点P是第二象限内抛物线上的动点，其横坐标为t。
①设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F。求出当△CEF与△COD相似时点P的坐标；
②是否存在一点P，使△PCD的面积最大？若存在，求出△PCD面积的最大值；若不存在，请说明理由。
如图，已知A（﹣4，
），B（﹣1，2）是一次函数y=kx+b与反比例函数y=
（m≠0，m＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D．
（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．
如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，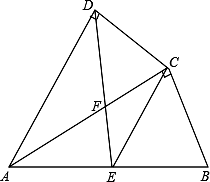
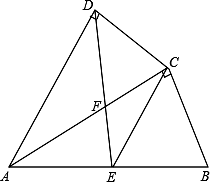
（1）求证：AC2＝AB•AD；
（2）求证：CE∥AD；
（3）若AD＝4，AB＝6，求
的值．
如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0．1m）．（参考数据：
≈1．414，
≈1．732）