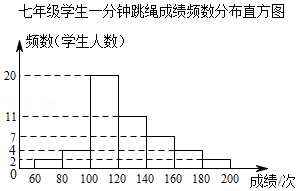
某校为了解七、八年级学生一分钟跳绳情况，从这两个年级随机抽取50名学生进行测试，并对测试成绩（一分钟跳绳次数）进行整理、描述和解析，下面给出了部分信息：
七、八年级学生一分钟跳绳成绩解析表
年级 |
平均数 |
中位数 |
众数 |
七 |
116 |
115 |
|
八 |
119 |
126 |
117 |
七年级学生一分钟跳绳成绩（数据分7组：，，，在这一组的是：
100 101 102 103 105 106 108 109 109 110 110 111 112 113 115 115 115 116 117 119
根据以上信息，回答下列问题：
（1）表中 ；
（2）在这次测试中，七年级甲同学的成绩122次，八年级乙同学的成绩125次，他们的测试成绩，在各自年级所抽取的50名同学中，排名更靠前的是 （填“甲”或“乙” ，理由是 ．
（3）该校七年级共有500名学生，估计一分钟跳绳不低于116次的有多少人？
现场学习：在△ABC中，AB、BC、AC三边的长分别为
、
、
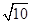，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
（1）△ABC的面积为： _________ ；
（2）若△DEF三边的长分别为、
、
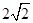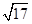，请在图1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；
（3）如图2，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13，10，17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．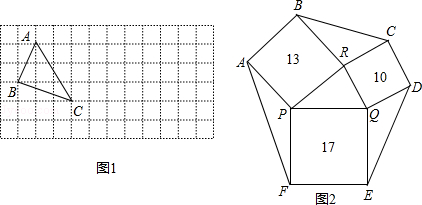
如图，直线
分别交x轴、y轴于A、B两点，线段AB的垂直平分线分别交x轴于点．求点C的坐标并求△ABC的面积．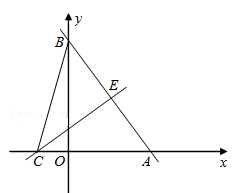
如图，在平行四边形ABCD中，E为BC边上的一点，连结AE、BD且AE=AB．
（1）求证：∠ABE=∠EAD；
（2）若∠AEB=2∠ADB，求证：四边形ABCD是菱形．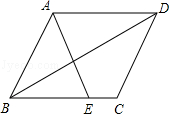
如图，△ACB和△ECD都是等腰直角三角形，△ACB的顶点A在△ECD的斜边DE的延长线上，求证：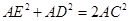
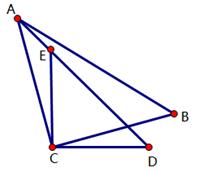
如图，（1）在梯形ABCD中，AB∥DC，若∠A＝∠B，求证：AD＝BC
（2）写出（1）的逆命题，并证明。