定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
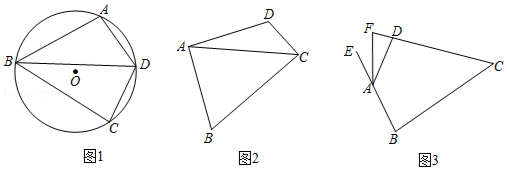
(1)如图1,点,,在上,的平分线交于点,连接,.
求证:四边形是等补四边形;
探究:
(2)如图2,在等补四边形中,,连接,是否平分?请说明理由.
运用:
(3)如图3,在等补四边形中,,其外角的平分线交的延长线于点,,,求的长.
如图是某住宅的平面结构示意图,图中标注了有关尺寸(墙体厚度勿略不计,单位: ).
).
(1)该住宅的面积是多少?
(2)该房的主人计划把卧室以外的地面都铺上地砖,若他所选的地砖的价格是60元/ ,他买地砖至少需要多少元?
,他买地砖至少需要多少元?
(1)利用如图4×4方格,作出面积为8平方单位的正方形;
(2)已知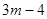 与
与 是N的平方根,求-2-N的立方根.
是N的平方根,求-2-N的立方根.
(1)已知 ,求:代数式
,求:代数式 的值;
的值;
(2)已知 ,求:代数式
,求:代数式 的值;
的值;
(3)已知 ,求:代数式
,求:代数式 的值.
的值.
化简:
(1)2(2x-3y)-(3x+2y+1);
(2)-(3a2-4ab)+[a2-2(2a+2ab)].
先观察下列等式,再回答问题:
①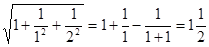 ;
;
②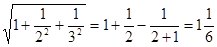 ;
;
③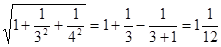 .
.
(1)根据上面三个等式提供的信息,请你猜想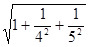 的结果;
的结果;
(2)请按照上面各等式反映的规律,试写出用字母表示的等式.