如图,已知反比例函数 和一次函数
和一次函数 的图象相交于第一象限内的点A,且点A的横坐标为1. 过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于第一象限内的点A,且点A的横坐标为1. 过点A作AB⊥x轴于点B,△AOB的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)若一次函数 的图象与x轴相交于点C,求∠ACO的度数;
的图象与x轴相交于点C,求∠ACO的度数;
(3)结合图象直接写出:当 >
> >0 时,x的取值范围.
>0 时,x的取值范围.
先化简再求值 ,其中
,其中 ,
,
如图一条抛物线 (a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是_______________三角形;
(2)若抛物线y=-x2+bx(b>0)的“抛物线三角形”是等腰直角三角形,求b的值;
(3)如图,△OAB是抛物线y=-x2+b′x(b′>0)的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由.
已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),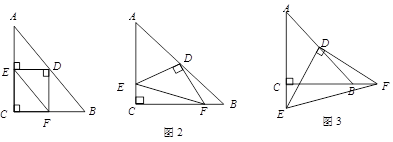
(1)易证 +
+ =
=
 .
.
(2) 当∠EDF绕
当∠EDF绕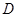 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立, 、
、 、
、 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
如图,用相同规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题: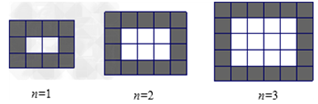
(1)在第n个图中,共有瓷砖______________________块,其中白色瓷砖______________块,黑色瓷砖_________________块(均用含n的代数式表示)
(2)按上述铺设方案,铺设一块这样的矩形地面共用了1056块瓷砖,求此时n的值;
(3)若黑瓷砖每块4元,白瓷砖每块3元,则问题(2)中,共花多少元购买瓷砖?
已知:如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点P,PD⊥AC于点D.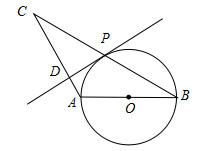
(1)求证:PD是⊙O的切线;
(2)若∠CAB=120°,AB=2,求BC的值.