今年是中华人民共和国建国70周年,襄阳市某学校开展了“我和我的祖国”主题学习竞赛活动.学校3000名学生全部参加了竞赛,结果所有学生成绩都不低于60分(满分100分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表.根据表中所给信息,解答下列问题:
成绩(分分组 |
频数 |
频率 |
15 |
0.30 |
|
0.40 |
||
10 |
||
5 |
0.10 |
(1)表中 , ;
(2)这组数据的中位数落在 范围内;
(3)判断:这组数据的众数一定落在范围内,这个说法 (填“正确”或“错误” ;
(4)这组数据用扇形统计图表示,成绩在范围内的扇形圆心角的大小为 ;
(5)若成绩不小于80分为优秀,则全校大约有 名学生获得优秀成绩.
已知抛物线y=ax2+bx+c ,当x=0时,有最小值为1 ;且在直线y=2上截得的线段长为4 .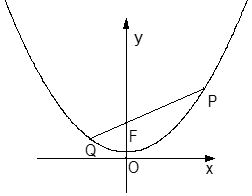
(1)求此抛物线的解析式;
(2)若点P是抛物线的任意一点,记点P到X轴的距离为d1,点P 与点 F (0,2)的距离为d 2,猜想d1、 d 2的大小关系,并证明;
(3)若直线PF交此抛物线于另一点Q(异于P点)。 试判断以PQ为直径的圆与x 轴的位置关系,并说明理由。
先阅读下列材料,再解答后面的问题:
要求算式 的值,我们可以按照如下方法进行:
的值,我们可以按照如下方法进行:
设 =S①则有2(
=S①则有2( )= 2S
)= 2S
∴ = 2S②
= 2S②
②-①得: = S∴
= S∴ = S
= S
∴ 原式:  =
= 
㈠请你根据上述方法计算:  = 。
= 。
㈡ 2008年美国的金融危机引发了波及全世界的经济危机,我国也在此次经济危机中深受影响,为此2009年我国积极理性的放宽信贷,帮助我国企业、特别是中小企业度过难关,尽最大努力减少我国的失业率。某企业在应对此次危机时积极进取,决定贷款进行技术改造,现有两种方案,甲方案:一次性贷款10万元,第一年便可获利1万元,以后每年获利比前一年增加30%的利润;
乙方案:每年贷款1万元,第一年可获利1万元,以后每年获利比前一年增加5千元;
两种方案的使用期都是10年,到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算,
试比较两种方案中,10年的总利润,哪种获利更多?(结果精确到0.01)
(取1.0510 =" 1.629" , 1.310 =" 13.786" , 1.510 =" 57.665" )
( 注意:‘复利’的计算方法,例如:一次性贷款7万元,按年息5%的复利计算;⑴若1年后归还本息,则要还 元。⑵若2年后归还本息,则要还
元。⑵若2年后归还本息,则要还 元。⑶若3年后归还本息,则要还
元。⑶若3年后归还本息,则要还 元。 )
元。 )
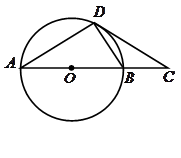
已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F ,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
⑴ 求证:△BCE≌△DCF;
⑵ OG与BF有什么数量关系?证明你的结论;
⑶ 若GE·GB=4-2 ,求 正方形ABCD的面积.
,求 正方形ABCD的面积.
某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
| 时间(天) |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 人数 |
1 |
2 |
4 |
5 |
7 |
11 |
8 |
6 |
4 |
2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
| 分组 |
频数 |
频率 |
| 3.5~5.5 |
3 |
0.06 |
| 5.5~7.5 |
9 |
0.18 |
| 7.5~9.5 |
0.36 |
|
| 9.5~11.5 |
14 |
|
| 11.5~13.5 |
6 |
0.12 |
| 合计 |
50 |
1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?
如图, 是⊙O的直径,
是⊙O的直径,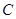 为
为 延长线上的一点,
延长线上的一点,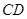 交⊙O于点
交⊙O于点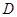 ,且
,且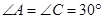 .
.
(1)求证: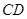 是⊙O的切线;
是⊙O的切线;
(2)请直接写出图中某3条线段之间的等量关系式,只要写出3个。(添加的辅助线不能用)