天水市某商店准备购进、两种商品,种商品每件的进价比种商品每件的进价多20元,用2000元购进种商品和用1200元购进种商品的数量相同.商店将种商品每件的售价定为80元,种商品每件的售价定为45元.
(1)种商品每件的进价和种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进、两种商品共40件,其中种商品的数量不低于种商品数量的一半,该商店有几种进货方案?
(3)“五一”期间,商店开展优惠促销活动,决定对每件种商品售价优惠元,种商品售价不变,在(2)的条件下,请设计出的不同取值范围内,销售这40件商品获得总利润最大的进货方案.
小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
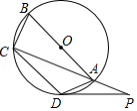
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 的长;
(Ⅱ)若 ,AD=AP,求证:PD是⊙O的切线.
我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:“有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?”试用列方程(组 解应用题的方法求出问题的解.
解应用题的方法求出问题的解.
如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)

如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
