为了解本校学生对新闻（A）、体育（B）、动画（C）、娱乐（D）、戏曲（E）五类电视节目的喜爱情况，课题小组随机选取该校部分学生进行了问卷调查，并根据调查结果绘制了两幅不完整的统计图，请根据统计图解答下列问题：
（1）本次接受问卷调查的学生有 名；
（2）补全条形统计图；
（3）扇形统计图中，类节目所对应的扇形圆心角的度数为 度；
（4）该校共有2000名学生，根据调查结果估计该校最喜爱新闻节目的学生数．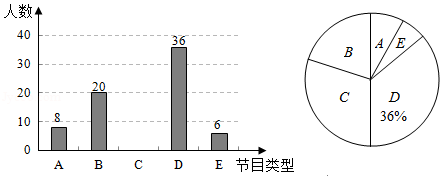
先化简，再求值：y (x＋y) +(x＋y)(x－y)－x2，其中x=－2， y=
某电视机生产厂家去年销往农村的某品牌电视机每台的售价y（元）与月份x之间满足函数关系
，去年的月销售量p（万台）与月份x之间成一次函数关系，其中两个月的销售情况如下表：
（1）求p与x之间的一次函数关系．
（2）求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？
（3）由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了
，且每月的销售量都比去年12月份下降了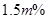
。国家实施“家电下乡”政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴。受此政策的影响，今年3月份至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元，求
的值（保留一位小数）
（参考数据：
，
，
，
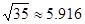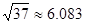销售金额=售价
销售量）
如图①，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（2，0）和点B（－6，0），与y轴交于点C．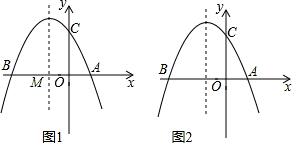
（1）求抛物线的解析式；
（2）设抛物线的对称轴与
轴交于点M ，在对称轴上存在点P，使△CMP为等腰三角形，请直接写出所有符合条件的点P的坐标．
（3）设点Q是抛物线对称轴上的一个动点，当点Q满足
最大时，求出Q点的坐标．
（4）如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．
已知∠GOH=90°，A、C分别是OG、OH上的点，且OA=OC=4，以OA为边长作正方形OABC．现将正方形OABC绕O点顺时针旋转，当A点第一次落在∠GOH的角平分线OP上时停止旋转；旋转过程中，AB边交OP于点M，BC边交OH于点N（如图2），
（1）旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；
（2）设△MBN的周长为p，在正方形OABC的旋转过程中，p值是否有变化？请证明你的结论．
如图，抛物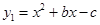线
经过直线
与坐标轴的两个交点A、B，此抛物线与
轴的另一个交点为C，抛物线顶点为D，
（1）求此抛物线的解析式；
（2）求四边形ADBC的面积；
（3）直接写出使
的x的取值范围．