某商场准备购进，两种书包，每个种书包比种书包的进价少20元，用700元购进种书包的个数是用450元购进种书包个数的2倍，种书包每个标价是90元，种书包每个标价是130元．请答案下列问题：
（1），两种书包每个进价各是多少元？
（2）若该商场购进种书包的个数比种书包的2倍还多5个，且种书包不少于18个，购进，两种书包的总费用不超过5450元，则该商场有哪几种进货方案？
（3）该商场按（2）中获利最大的方案购进书包，在销售前，拿出5个书包赠送给某希望小学，剩余的书包全部售出，其中两种书包共有4个样品，每种样品都打五折，商场仍获利1370元．请直接写出赠送的书包和样品中，种书包各有几个？
（本题8分）各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形。如何计算它的面积？奥地利数学家皮克（G.Pick，1859~1942）证明了格点多边形的面积公式：
，其中
表示多边形内部的格点数，
表示多边形边界上的格点数，S表示多边形的面积。如图，
，
，
。
（1）请在图甲中画一个格点正方形，使它内部只含有4个格点，并写出它的面积；
（2）请在图乙中画一个格点三角形，使它的面积为
，且每条边上除顶点外无其它格点。（注：图甲、图乙在答题纸上）
（本题8分）某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核。甲、乙、丙各项得分如下表：
| 笔试 |
面试 |
体能 |
|
| 甲 |
83 |
79 |
90 |
| 乙 |
85 |
80 |
75 |
| 丙 |
80 |
90 |
73[:m] |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序；
（2）该公司规定：笔试、面试、体能分分别不得低于80分、80分、70分，并按60%，30%，10%的比例计入总分。根据规定，请你说明谁将被录用。
（本题8分）如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D。
（1）求证：AB=CD；
（2）若AB=CF，∠B=30°，求∠D的度数。
（本题10分）（1）计算：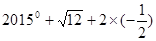
（2）化简：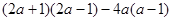
（本小题满分11分）如图，E、F分别是正方形ABCD的边DC、CB上的点，且DE=CF，以AE为边作正方形AEHG，HE与BC交于点Q，连接DF.
（1）求证：△ADE≌△DCF；
（2）若E是CD的中点，求证：Q为CF的中点；
（3）连接AQ，设S△CEQ=S1，S△AED=S2，S△EAQ=S3，在（2）的条件下，判断S1+S2=S3是否成立？并说明理由．