判断下列方程的解是正数、负数、还是0:
(1)4x=-16;(2)-3x=18;(3)-9x=-36;(4)-5x=0;
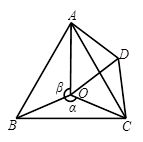
如图,点 是等边
是等边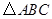 内一点,
内一点,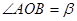 ,
, 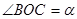 .将
.将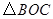 绕点
绕点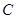 按顺时针方向旋转
按顺时针方向旋转 得
得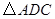 ,连接
,连接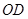 .
.
(1)当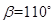 ,
,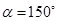 时,试判断
时,试判断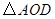 的形状,并说明理由.
的形状,并说明理由.
(2)请写出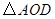 是等边三角形时
是等边三角形时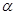 、
、 的度数.
的度数.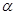 = 度;
= 度;  =度.
=度.
(3)探究:若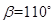 ,则
,则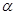 为多少度时,
为多少度时,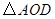 是等腰三角形?
是等腰三角形?
(只要写出探究结果)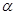 = ;
= ;
已知关于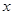 的一元二次方程
的一元二次方程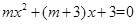 .
.
(1)求证:方程有两个实数根;
(2)当此方程有一个根是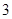 时,求关于
时,求关于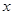 的二次函数
的二次函数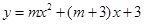 的表达式;
的表达式;
(3)在(2)的条件下,若点A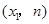 与点B
与点B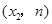 (
(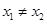 )在关于
)在关于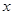 的二次函数
的二次函数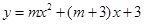 的图象上,将此二次函数的图象在
的图象上,将此二次函数的图象在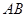 上方的部分沿
上方的部分沿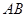 翻折,图象的其它部分保持不变,得到一个新图象,当这个新图象与x轴恰好只有两个公共点时,n的取值范围是_________________________________________.
翻折,图象的其它部分保持不变,得到一个新图象,当这个新图象与x轴恰好只有两个公共点时,n的取值范围是_________________________________________.
小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 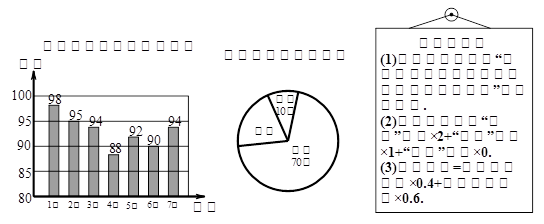
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
如图,在直角坐标系xoy中,点A是反比例函数y1= 的图象上一点,AB⊥x轴的正半轴于点B,C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AO D=4.
的图象上一点,AB⊥x轴的正半轴于点B,C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,并交y轴于点D(0,-2),若S△AO D=4.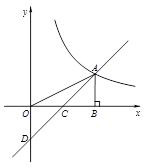
(1)求反比例函数和一次函数的表达式;
(2)观察图象,请指出在y轴的右侧,当y1>y2时x的取值范围.
如图,在□ABCD中,E是对角线AC的中点,EF⊥AD于F,∠B=60°,AB=4,∠ACB=45°,求DF的长.