如图,已知直线与轴交于点,与轴交于点,线段的长是方程的一个根,.请答案下列问题:
(1)求点,的坐标;
(2)直线交轴负半轴于点,交轴正半轴于点,交直线于点.若是的中点,,反比例函数图象的一支经过点,求的值;
(3)在(2)的条件下,过点作,垂足为,点在直线上,点在直线上.坐标平面内是否存在点,使以,,,为顶点的四边形是正方形?若存在,请写出点的个数,并直接写出其中两个点的坐标;若不存在,请说明理由.

.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.
(1)改善后滑滑板会加长多少?(精确到0. 1)
(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长空地,像这样改造是否可行说明理由?(参考
 )
)
从车站到书城有A1、A2、A3、A4四条路线可走,从书城到广场有B1、B2、B3三条路线可走,现让你随机选择一条从车站出发经过书城到达广场的行走路线.画树状图分析你所有可能选择的路线.
你恰好选到经过路线B1的概率是多少?
(1)请在方格纸上建立平面直角坐标系,使
 ,并求出
,并求出 点坐标;
点坐标;(2)以原点
 为位似中心,相似比为2:1,在第一象限内将
为位似中心,相似比为2:1,在第一象限内将 放大,画出放大后的图形
放大,画出放大后的图形 ;
;
计算:(1)
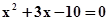
(2)(p-2010)0 +(sin60°)-1-︱tan30°-
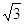 ︱+
︱+ 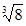 .
.
已知:等腰梯形ABCD,AD∥BC,AB=DC=5,AD=6,BC=12,动点P从点D出发沿DC以每秒1个单位向终点C运动,点Q从点C出发沿CB以每秒2个单位向B运动,当点P到达C时,点Q随之停止运动,设点P运动的时间为t秒.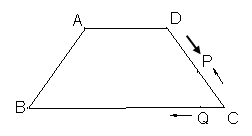
(1)求梯形ABCD面积.
(2)当PQ∥AB时,求t.
(3) 当点P、Q、C三点构RT△时,求t值.