.如图,某幼儿园为了加强安全管理，决定将园内的滑滑板的倾角由45º降为30º，已知原滑滑板AB的长为5米，点D、B、C在同一水平地面上．
（1）改善后滑滑板会加长多少？（精确到0. 1）
（2）若滑滑板的正前方能有3米长的空地就能保证安全，原滑滑板的前方有6米长空地，像这样改造是否可行说明理由？(参考
)
已知：一次函数
与
的图像的交点的坐标为P（1，–2）．求:方程组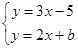
的解和b的值．
如图，已知△ABC的三个顶点的坐标都在格点上，分别为A（－2,3）、B（－6,0） 、C（－1,0）．
（1）请将点A、B、C的纵坐标分别乘以-1后得到点A′、B′、C ′描在坐标系中，并顺次连接A′、B′、C ′得到△A′B′C ′；
（2）请问△A′B′C ′与△ABC有怎样的位置关系？
先观察：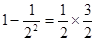
，
，
，…
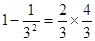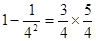（1）探究规律填空：
=×；
（2）计算：
下表给出了某班6名同学身高情况（单位：cm）
（1）完成表中空的部分；
（2）他们6人中最高身高比最矮身高高多少？
（3）如果身高达到或超过平均身高时叫达标身高，那么这6个同学身高的达标率是多少？（用小数表示，精确到小数点后两位）
现在5袋小麦重依次为183千克，176千克，185千克，178千克，181千克，以181千克为准．超过的斤数记为正数，不足的斤数记为负数，那么这5袋小麦与标准重量相比，超出或不足千克数依次为多少？这5袋小麦总重量为多少克？