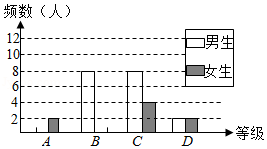
某校对九年级学生进行一次综合文科中考模拟测试,成绩分为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用、、、表示),等级:,等级:,等级:,等级:.该校随机抽取了一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.
等级 |
频数(人数) |
频率 |
16 |
||
4 |
请你根据统计图表提供的信息解答下列问题:
(1)上表中的 , , .
(2)本次调查共抽取了多少名学生?请补全条形图.
(3)若从等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.
计算:
用心算一算:
用心算一算:
作图分析题
已知:∠AOB,点P在OA上,请以P为顶点,PA为一边作∠APC=∠O
(不写作法,但必须保留作图痕迹)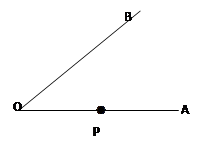
如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒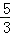 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
(1)当t=3秒时.直接写出点N的坐标,并求出经过O、A、N三点的抛物线的解析式;
(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;
(3)当t为何值时,△MNA是一个等腰三角形?