如图，在平面直角坐标系中，直角三角形AOB的顶点A、B分别落在坐标轴上．O为原点，点A的坐标为（6，0），点B的坐标为（0，8）．动点M从点O出发．沿OA向终点A以每秒1个单位的速度运动，同时动点N从点A出发，沿AB向终点B以每秒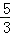
个单位的速度运动．当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒（t＞0）．
（1）当t=3秒时．直接写出点N的坐标，并求出经过O、A、N三点的抛物线的解析式；
（2）在此运动的过程中，△MNA的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由；
（3）当t为何值时，△MNA是一个等腰三角形？
已知数轴上有A、B、C三点，分别表示有理数-26，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．
（1）用含t的代数式表示P到点A和点C的距离：PA=________，PC=_____________
（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后，请用t的代数式表示P、Q两点间的距离。（友情提醒：注意考虑P、Q的位置）
（1）如图1，正方形ABCD和CEFG的边长分别为m、n，用含m、n的代数式表示△AEG的面积。
（2）如图2，正方形ABCD和CEFG的边长分别为m、n，用含m、n的代数式表示△DBF的面积。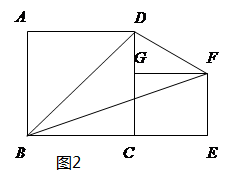
（3）如图，正方形ABCD、正方形CEFG和正方形MNHF的位置如图所示，点G在线段AN上，已知正方形CEFG的边长为6，则△AEN的面积为（请直接写出结果，不需要过程）
某商场购进一批西服，进价为每套250元，原定每套以290元的价格销售，这样每天可销售200套。如果每套比原销售价降低10元销售，则每天可多销售100套。该商场为了确定销售价格，作了如下测算，请你参加测算，并由此归纳得出结论（每套西服的利润=每套西服的销售价－每套西服的进价）.
1、按原销售价销售，每天可获利润元。
2、若每套降低10元销售，每天可获利润元。
3、如果每套销售价降低10元，每天就多销售100套，每套销售价降低20元，每天就多销售200套。按这种方式: 若每套降低10x元
（1）每套的销售价格为元；（用代数式表示）
（2）每天可销售套西服。（用代数式表示）
（3）每天共可以获利润元。（用代数式表示）
已知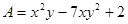
，
，
（1）求
（2）当
满足
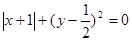时，请你求出（1）中的代数式的值。
化简：（每小题4分，共12分）
（1）
；
（2）
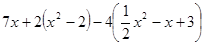
（3）先化简再求值2（3b2－a3b）－3（2b2－a2b－a3b）－4a2b，其中a＝－
，b＝8.