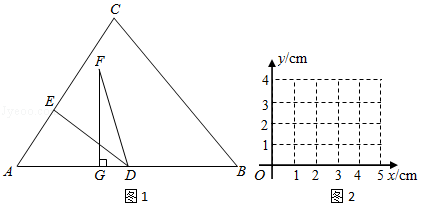
如图1,在 中, , , ,点D为AB的中点,线段 上有一动点E,连接DE,作DA关于直线DE的对称图形,得到 ,过点F作 于点G.设A、E两点间的距离为 , 两点间的距离为
小军根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小军的探究过程,请补充完整.
(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
|
x/cm |
0 |
0.51 |
1.03 |
1.41 |
1.50 |
1.75 |
2.20 |
2.68 |
3.00 |
3.61 |
4.10 |
4.74 |
5.00 |
|
y/cm |
0 |
0.94 |
1.91 |
2.49 |
|
2.84 |
3.00 |
2.84 |
2.60 |
2.00 |
1.50 |
0.90 |
0.68 |
请你通过计算补全表格;
(2)描点、连线:在平面直角坐标系 中(如图2),描出表中各组数值所对应的点 ,并画出y关于x的图象;
(3)探究性质:随着x值的不断增大,y的值是怎样变化的? ;
(4)解决问题:当 时,FG的长度大约是 cm(保留两位小数).
为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
|
名称 |
红外线体温检测仪 |
|
安装示意图 |
|
|
技术参数 |
探测最大角: |
|
探测最小角: |
|
|
安装要求 |
本设备需安装在垂直于水平地面AC的支架CP上 |
根据以上内容,解决问题:
学校要求测温区域的宽度AB为4m,请你帮助学校确定该设备的安装高度OC.
(结果精确到0.1m,参考数据: ,t , , , )
为培养学生正确的劳动价值观和良好劳动品质,加强新时代中学生劳动教育,某校八年级(1)班对本班35名学生进行了劳动能力量化评估和近一周家务劳动总时间调查,并对相关数据进行了收集、整理和分析,研究过程中的部分数据如下:
信息一:劳动能力量化评估的成绩采用十分制,得分均为整数;
信息二:

信息三:
近一周家务劳动时间分布表
|
时间/小时 |
|
|
|
|
|
|
人数/人 |
5 |
8 |
12 |
7 |
3 |
信息四:
劳动能力量化成绩与近一周家务劳动总时间统计表
|
成绩/分 人数 时间/小时 |
6 |
7 |
8 |
9 |
10 |
|
|
4 |
1 |
0 |
0 |
0 |
|
|
0 |
6 |
1 |
1 |
0 |
|
|
0 |
0 |
9 |
3 |
0 |
|
|
0 |
1 |
1 |
3 |
2 |
|
|
0 |
0 |
0 |
1 |
2 |
根据以上信息,解决下列问题:
(1)直接从信息二的统计图中“读”出八年级(1)班劳动能力量化成绩的平均分为 分;
(2)请你判断下列说法合理吗?(请在横线上填写“合理”或“不合理”)
①规定劳动能力量化成绩8分及以上为合格,八年级(1)班超过半数的学生达到了合格要求: .
②班主任对近一周家务劳动总时间在4小时以上,且劳动能力量化成绩取得10分的学生进行表彰奖励,恰有3人获奖: .
③小颖推断劳动能力量化成绩为8分的同学近一周家务劳动总时间主要分布在 的时间段: .
(3)结合以上信息,你认为普遍情况下参加家务劳动的时间与劳动能力之间具有怎样的关系?
如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于 , 两点,与x轴,y轴分别交于点C,D,连接OA,OB.
(1)求反比例函数 和一次函数 的表达式;
(2)求 的面积.
