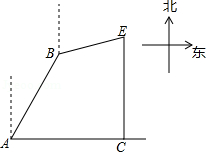
如图,海岛 在海岛 的北偏东30方向,且与海岛 相距20海里,一艘渔船从海岛 出发,以5海里 时的速度沿北偏东 方向航行,同时一艘快艇从海岛 出发,向正东方向航行.2小时后,快艇到达 处,此时渔船恰好到达快艇正北方向的 处.
(1)求 的度数;
(2)求快艇的速度及 , 之间的距离.
(参考数据: , , ,
下表给出了某班6名同学身高情况(单位:cm)
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6个同学身高的达标率是多少?(用小数表示,精确到小数点后两位)
现在5袋小麦重依次为183千克,176千克,185千克,178千克,181千克,以181千克为准.超过的斤数记为正数,不足的斤数记为负数,那么这5袋小麦与标准重量相比,超出或不足千克数依次为多少?这5袋小麦总重量为多少克?
先化简再求值(每小题6分,共12分)
(1)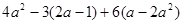 ,其中
,其中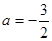 ;
;
(2)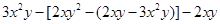 ,其中
,其中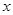 =3,
=3,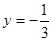 .
.
如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(一定保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.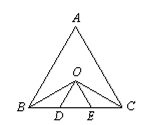
(1)试判定△ODE的形状。并说明你的理由.
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.