如图，在△ABC中，AB=AC，∠ABC=72°．
（1）用直尺和圆规作∠ABC的平分线BD交AC于点D（一定保留作图痕迹，不要求写作法）；
（2）在（1）中作出∠ABC的平分线BD后，求∠BDC的度数．
（每小题6分，共12分）解方程
（1）解方程：
（2）先化简，再求值：2(5a2-7ab+9b2)-3(14a2-2ab+3b2)，其中a=
．
（每题6分，共12分）计算：
（1）
（2）
+
在平面直角坐标系xOy中，已知抛物线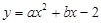
经过（2，1）和（6，－5）两点．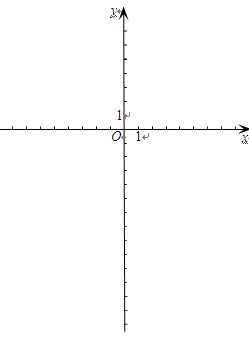
（1）求抛物线的解析式；
（2）设此抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于C点，点P是在直线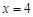
右侧的此抛物线上一点，过点P作PM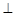
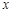轴，垂足为M. 若以A、P、M为顶点的三角形与△OCB相似，求点P的坐标；
（3）点E是直线BC上的一点，点F是平面内的一点，若要使以点O、B、E、F为顶点的四边形是菱形，请直接写出点F的坐标.
如图，在平面直角坐标系xOy中，已知点B的坐标为（2，0），点C的坐标为（0，8），sin∠CAB=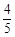
, E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连结CE.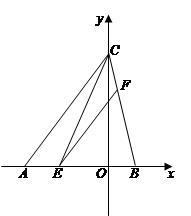
（1）求AC和OA的长；
（2）设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式；
（3）在（2）的条件下试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．
已知抛物线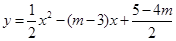
．
（1） 求证：无论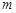
为任何实数，抛物线与
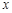轴总有两个交点；
（2） 若A
、B
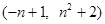是抛物线上的两个不同点，求抛物线的解析式和
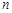的值；
（3） 若反比例函数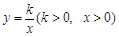
的图象与（2）中的抛物线在第一象限内的交点的横坐标为
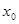，且满足2<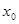<3，求k的取值范围.