为了抗击新冠疫情，我市甲、乙两厂积极生产了某种防疫物资共50-优题课

游客

题文

为了抗击新冠疫情，我市甲、乙两厂积极生产了某种防疫物资共500吨，乙厂的生产量是甲厂的2倍少100吨．这批防疫物资将运往 $A$ 地240吨， $B$ 地260吨，运费如下表（单位：元 $/$ 吨）．

目的地

生产厂

$A$

$B$

甲

乙

（1）求甲、乙两厂各生产了这批防疫物资多少吨？

（2）设这批物资从乙厂运往 $A$ 地 $x$ 吨，全部运往 $A$ ， $B$ 两地的总运费为 $y$ 元．求 $y$ 与 $x$ 之间的函数关系式，并设计使总运费最少的调运方案；

（3）当每吨运费均降低 $m$ 元 $(0 < m ⩽ 15$ 且 $m$ 为整数）时，按（2）中设计的调运方案运输，总运费不超过5200元．求 $m$ 的最小值．

科目数学题型解答题难度中等

知识点：二元一次方程组的应用一元一次不等式组的应用一次函数的应用

登录免费查看答案和解析

相关试题

如图，已知CB是⊙O的弦，CD是⊙O的直径，点A为CD延长线上一点，BC=AB，∠CAB=30°．
（1）求证:AB是⊙O的切线；（2）若⊙O的半径为2，求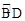的长．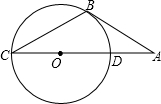

解方程：．

（1）计算：；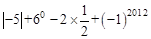
（2）先化简，再求值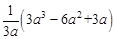：，其中．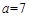

如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm，D、E分别为边AB、BC的中点，连结DE，点P从点A出发，沿折线AD－DE－EB运动，到点B停止．点P在AD上以cm/s的速度运动，在折线DE－EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t(s).

（1）当点P在线段DE上运动时，线段DP的长为______cm,（用含t的代数式表示）．
（2）当点N落在AB边上时，求t的值．
（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm²），求S与t的函数关系式．
（4）连结CD．当点N于点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M-N-M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中心处．直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．

如图，在平面直角坐标系中，直线y=－2x+42交x轴与点A,交直线y=x于点B,抛物线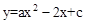分别交线段AB、OB于点C、D，点C和点D的横坐标分别为16和4，点P在这条抛物线上．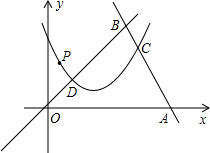

（1）求点C、D的纵坐标．
（2）求a、c的值．
（3）若Q为线段OB上一点，且P、Q两点的纵坐标都为5，求线段PQ的长．
（4）若Q为线段OB或线段AB上的一点，PQ⊥x轴，设P、Q两点之间的距离为d（d＞0），点Q的横坐标为m，直接写出d随m的增大而减小时m的取值范围．
（参考公式：二次函数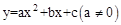图像的顶点坐标为）

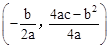试卷网试题网古诗词网作文网范文网