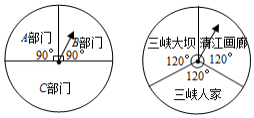
宜昌景色宜人，其中三峡大坝、清江画廊、三峡人家景点的景色更是美不胜收．某民营单位为兼顾生产和业余生活，决定在下设的 ， ， 三部门利用转盘游戏确定参观的景点．两转盘各部分圆心角大小以及选派部门、旅游景点等信息如图．
（1）若规定老同志相对偏多的部门选中的可能性大，试判断这个部门是哪个部门？请说明理由；
（2）设选中 部门游三峡大坝的概率为 ，选中 部门游清江画廊或者三峡人家的概率为 ，请判断 ， 大小关系，并说明理由．
统计2010年上海世博会前20天日参观人数，得到如下频数分布表和频
数分布直方图（部分未完成）：
（1）请补全频数分布表和频数分布直方图；
（2）求出日参观人数不低于22万的天数所占的百分比；
（3）利用以上信息，试估计上海世博会（会期184天）的参观总人数.
如图，在
和
中，
、
交于点M.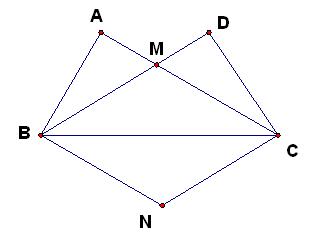
（1）求证：≌；
（2）作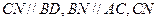
交
于点N，四边形BNCM是什么四边形？请证明你的结论.
请你先化简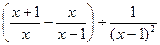
，再从0，
， 2，1中选择一
个合适的数代入，求出这个代数式的值.
已知，边长为5的正方形ABCO在如图所示的直角坐标系中，点
M（t，0）为x轴上一动点，过A作直线MC的垂线交y轴于点N．
（1）当t=2时，求直线MC的解析式；
（2）设△AMN的面积为S，当S＝3时，求t的值；
（3）取点P（1，y），如果存在以M、N、C、P为顶点的四边形是等腰梯形，当t＜0时，甲同学说：y与t应同时满足方程t2－yt－5＝0和y2－2t2－10y＋26＝0；乙同学说：y与t应同时满足方程t2－yt－5＝0和y2＋8t－24＝0，你认为谁的说法
正确，并说明理由．再直接写出t＞0时满足题意的一个点P的坐标．
如图，抛物线F：y＝ax2＋bx＋c的顶点为P，抛物线F与
轴交于点A，
过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得
到抛物线F ′：
y＝a′x2＋b′x＋c′，抛物线F ′与x轴的另一个交点为C．
（1）当a＝1，b＝－2，c＝3时，
①写出点D的坐标▲；②求b: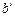
的值；
（2）若a、b、c满足b2＝ac，探究b: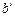的值是否为定值？若是定值请求出这个定值；若不是请说明理由．