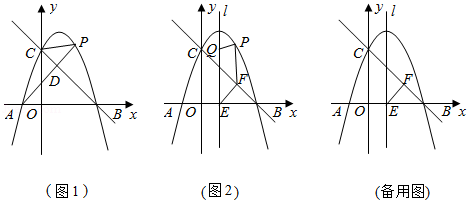
如图1,抛物线 与 轴交于 , ,与 轴交于点 .已知直线 过 , 两点.
(1)求抛物线和直线 的表达式;
(2)点 是抛物线上的一个动点.
①如图1,若点 在第一象限内,连接 ,交直线 于点 .设 的面积为 , 的面积为 ,求 的最大值;
②如图2,抛物线的对称轴 与 轴交于点 ,过点 作 ,垂足为 .点 是对称轴 上的一个动点,是否存在以点 , , , 为顶点的四边形是平行四边形?若存在,求出点 , 的坐标;若不存在,请说明理由.
某校在一次大课间活动中,采用了四种活动形式: 、跑步, 、跳绳, 、做操, 、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.
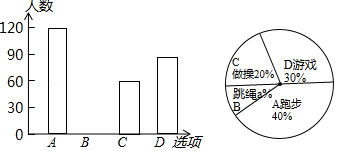
请结合统计图,回答下列问题:
(1)本次调查学生共 人, ,并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在 、 、 、 四种活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
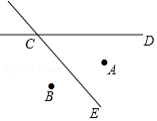
两个城镇 , 与一条公路 ,一条河流 的位置如图所示,某人要修建一避暑山庄,要求该山庄到 , 的距离必须相等,到 和 的距离也必须相等,且在 的内部,请画出该山庄的位置 .(不要求写作法,保留作图痕迹.
如图,点 , 分别在菱形 的边 , 上,且 .
求证: .

如图,13个边长为1的小正方形,排列形式如图,把它们分割,使分割后能拼成一个大正方形.请在如图所示的网格中(网格的边长为 中,用直尺作出这个大正方形.

如图,抛物线 与 轴交于 , 两点,与直线 交于 , 两点,直线 与抛物线的对称轴交于点 .
(1)求抛物线的解析式;
(2)若点 在直线 上方的抛物线上运动.
①点 在什么位置时, 的面积最大,求出此时点 的坐标;
②当点 与点 重合时,连接 ,将 补成矩形,使 上的两个顶点成为矩形一边的两个顶点,第三个顶点落在矩形这一边的对边上,求出矩形未知顶点的坐标.
