定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为"直角等邻对补"四边形,简称"直等补"四边形.
根据以上定义,解决下列问题:
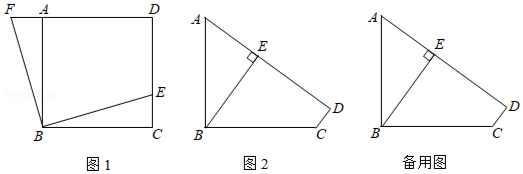
(1)如图1,正方形 中, 是 上的点,将 绕 点旋转,使 与 重合,此时点 的对应点 在 的延长线上,则四边形 为"直等补"四边形,为什么?
(2)如图2,已知四边形 是"直等补"四边形, , , ,点 到直线 的距离为 .
①求 的长;
②若 、 分别是 、 边上的动点,求 周长的最小值.
在平面直角坐标系中,已知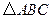 三个顶点的坐标分别为
三个顶点的坐标分别为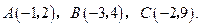
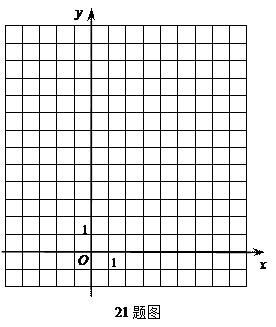
(1)画出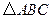 ,并求出
,并求出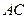 所在直线的解析式。
所在直线的解析式。
(2)画出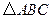 绕点
绕点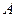 顺时针旋转
顺时针旋转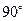 后得到的
后得到的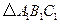 ,并求出
,并求出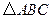 在上述旋转过程中扫过的面积。
在上述旋转过程中扫过的面积。
如图,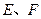 是平行四边形
是平行四边形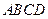 的对角线
的对角线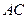 上的点,
上的点,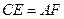 ,请你猜想:线段
,请你猜想:线段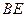 与线段
与线段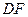 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。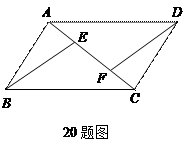
我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了 (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着 展开式中的系数等等。
展开式中的系数等等。
(1)根据上面的规律,写出 的展开式。
的展开式。
(2)利用上面的规律计算:
计算: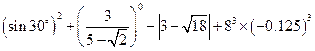
如图,抛物线与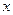 轴交于
轴交于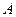 (
(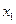 ,0)、
,0)、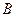 (
(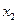 ,0)两点,且
,0)两点,且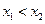 ,与
,与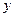 轴交于点
轴交于点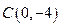 ,其中
,其中 是方程
是方程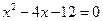 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点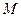 是线段
是线段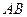 上的一个动点,过点
上的一个动点,过点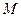 作
作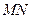 ∥
∥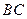 ,交
,交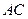 于点
于点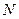 ,连接
,连接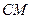 ,当
,当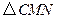 的面积最大时,求点
的面积最大时,求点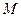 的坐标;
的坐标;
(3)点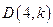 在(1)中抛物线上,点
在(1)中抛物线上,点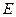 为抛物线上一动点,在
为抛物线上一动点,在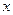 轴上是否存在点
轴上是否存在点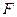 ,使以
,使以 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点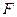 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。