如图,一次函数 的图象与反比例函数 为常数且 的图象相交于 , 两点.
(1)求反比例函数的表达式;
(2)将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求 的值.

如图,一次函数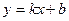 的图象与反比例函数
的图象与反比例函数 图象交于A(-2,1)、B(1,n)两点。
图象交于A(-2,1)、B(1,n)两点。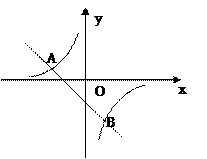
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。

矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm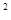
(1)求y与x之间的关系式.
(2)求当边长增加多少时,面积增加8 cm
(本题满分12分)如图,抛物线y=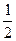 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).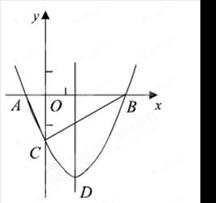
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;

⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
(本题满分12分)某商场购进一批单价为16元日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数Y(件)是价格X(元/件)的一次函数 (1)试求Y与X之间的关系式。
(2)在商品积压,且不考虑其它因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本)