我们不妨约定:若某函数图象上至少存在不同的两点关于原点对称,则把该函数称之为“函数”,其图象上关于原点对称的两点叫做一对“点”.根据该约定,完成下列各题.
(1)在下列关于的函数中,是“函数”的,请在相应题目后面的括号中打“”,不是“函数”的打“”.
① ;
② ;
③ .
(2)若点与点是关于的“函数” 的一对“点”,且该函数的对称轴始终位于直线的右侧,求,,的值或取值范围.
(3)若关于的“函数” ,,是常数)同时满足下列两个条件:①,②,求该“函数”截轴得到的线段长度的取值范围.
如图,在△ABC中,AB=AC,∠ABC=72°,
(1)用直尺和圆规作∠ABC的平分线BD,交AC于点D.(保留作图痕迹,不要求写作法)
(2)在(1)中作出∠ABC的平分线后,求∠BDC的度数.
已知线段AB=8 cm,在直线AB上有一点C,且BC=4 cm,点M是线段AC的中点, 求线段AM的长.
如图,已知a∥b,小亮把三角板的直角顶点放在直线b上,若∠1=40°,则∠2的度数为________.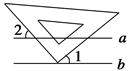
如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.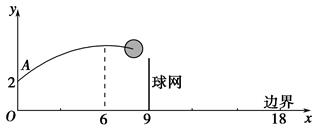
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
如图,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2 cm的速度匀速运动,Q在边BC上沿BC方向以每秒1 cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).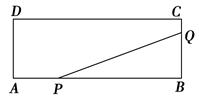
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.