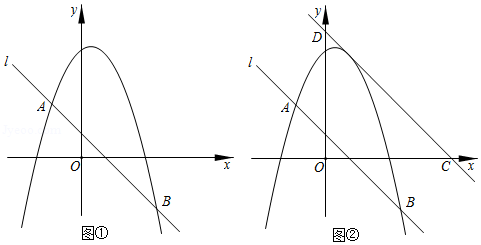
如图①,二次函数的图象与直线交于、两点.点是轴上的一个动点,过点作轴的垂线交直线1于点,交该二次函数的图象于点,设点的横坐标为.
(1) , ;
(2)若点在点的上方,且,求的值;
(3)将直线向上平移4个单位长度,分别与轴、轴交于点、(如图②.
①记的面积为,的面积为,是否存在,使得点在直线的上方,且满足?若存在,求出及相应的,的值;若不存在,请说明理由.
②当时,将线段绕点顺时针旋转得到线段,连接、、.若,直接写出直线与该二次函数图象交点的横坐标.
解下列方程(每小题5分,共10分)
(1)、 

某地生产的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨.该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行.受季节等条件限制,公司必须在15天之内将这批蔬菜全部销售或加工完毕.为此,公司研制了三种加工方案:
方案一:将蔬菜全部进行粗加工.
方案二:尽可能多地对蔬菜进行精加工,没来得及进行加工的蔬菜在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好用15天完成.
你认为选择哪种方案获利最多?为什么?
阅读以下例题:“解不等式: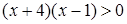
解:①当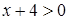 ,则
,则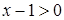 当若
当若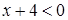 ,则
,则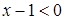
即可以写成: 即可以写成:
即可以写成:
解不等式组得: 解不等式组得:
解不等式组得:
综合以上两种情况:不等式解集: 或
或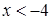
(以上解法依据:若 ,则
,则 同号)请你模仿例题的解法,解不等式:
同号)请你模仿例题的解法,解不等式:
(1) (2)
(2)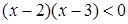
某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
| 类 别 |
电视机 |
洗衣机 |
| 进价(元/台) |
1800 |
1500 |
| 售价(元/台) |
2000 |
1600 |
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
2008年5月12日,汶川发生了里氏8.0级地震,给当地人民造成了巨大的损失.某中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:
老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:二班的捐款金额比三班的捐款金额多300元;
信息三:一班学生平均每人捐款的金额大于48元,小于51元.
请根据以上信息,帮助老师解决:
(1)二班与三班的捐款金额各是多少元?
(2)一班的学生人数是多少?