为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了"垃圾分类知识竞赛",为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是 .(填"方案一"、"方案二"或"方案三"
(2)学校根据样本数据,绘制成下表 分及以上为"优秀",60分及以上为"及格"
样本容量 |
平均分 |
及格率 |
优秀率 |
最高分 |
最低分 |
100 |
93.5 |
|
|
100 |
80 |
分数段统计(学生成绩记为 |
|||||
分数段 |
|
|
|
|
|
频数 |
0 |
5 |
25 |
30 |
40 |
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到"优秀"的学生总人数.
(本题10分)腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为 ,底部B点的俯角为
,底部B点的俯角为 ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为 (如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据 ).
).
(本题8分)某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手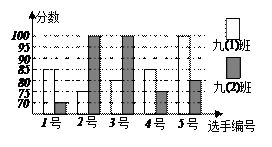
参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
(1)根据左图填写 下表
下表
| 平均分(分) |
中位数(分) |
众数(分) |
|
| 九(1)班 |
85 |
85 |
|
| 九(2)班 |
85 |
80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪
个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出2人参
加决赛,你认为哪个班的实力更强一些,说明理由.
(本题8分)如图,四边形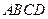 中,
中,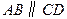 ,
,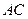 平分
平分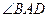 ,
,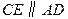 交
交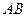 于
于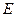 .
.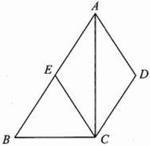
(1)求证:四边形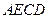 是菱形;
是菱形;
(2)若点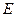 是
是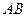 的中点,试判断
的中点,试判断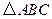 的形状,并说明理由.
的形状,并说明理由.
学了《认识事件的可能性》,林林想到了小时候常玩“锤子、剪刀、布”,他想两个人一起玩,有哪些可能情况?请你用列表的方式帮他写出来
把1、2、3三个数组成一个三位数,共有多少种可能?