一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：
摸球的次数 |
200 |
300 |
400 |
1000 |
1600 |
2000 |
摸到白球的频数 |
72 |
93 |
130 |
334 |
532 |
667 |
摸到白球的频率 |
0.3600 |
0.3100 |
0.3250 |
0.3340 |
0.3325 |
0.3335 |
（1）该学习小组发现，摸到白球的频率在一个常数附近摆动，这个常数是 ．（精确到 ，由此估出红球有 个．
（2）现从该袋中摸出2个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到1个白球，1个红球的概率．
判断下列命题的真假，并说明理由．
（1）两个无理数的和仍然是无理数．
（2）如果a＞b，那么1﹣2a＜1﹣2b．
阅读下面的文字，解答问题．
大家知道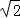
是无理数，而无理数是无限不循环小数，因此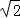的小数部分我们不可能全部地写出来，但是由于1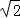＜＜2，所以
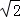的整数部分为1，将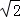减去其整数部分1，差就是小数部分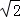﹣1，根据以上的内容，解答下面的问题：
（1）
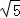的整数部分是，小数部分是；
（2）1+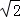的整数部分是，小数部分是；
（3）若设2+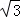
整数部分是x，小数部分是y，求x﹣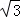y的值．
用适当的符号表示下列关系：
（1）x的
与x的2倍的和是非正数；
（2）一枚炮弹的杀伤半径不小于300米；
（3）三件上衣与四条长裤的总价钱不高于268元；
（4）明天下雨的可能性不小于70%；
（5）小明的身体不比小刚轻．
已知有理数m，n的位置在数轴上如图所示，用不等号填空．
（1）n﹣m0；（2）m+n0；（3）m﹣n0；（4）n+10；（5）m•n0；
（6）m+10．
在数轴上表示不等式﹣3≤x＜6的解集和x的下列值：﹣4，﹣2，0，
，7，并利用数轴说明x的这些数值中，哪些满足不等式﹣3≤x＜6，哪些不满足？