将4张印有"梅""兰""竹""菊"字样的卡片（卡片的形状、大小、质地都相同）放在一个不透明的盒子中，将卡片搅匀．
（1）从盒子中任意取出1张卡片，恰好取出印有"兰"字的卡片的概率为 ．
（2）先从盒子中任意取出1张卡片，记录后放回并搅匀，再从中任意取出1张卡片，求取出的两张卡片中，至少有1张印有"兰"字的概率（请用画树状图或列表等方法求解）．
在如图所示的平面直角坐标系中，直线AB：y=k1x+b1与直线AD：y=k2x+b2相交于点A（1，3），且点B坐标为（0，2），直线AB交x轴负半轴于点C，直线AD交x轴正半轴于点D．
（1）求直线AB的函数解析式；
（2）根据图象直接回答，不等式k1x+b1＜k2x+b2的解集；
（3）若△ACD的面积为9，求直线AD的函数解析式；
（4）若点M为x轴一动点，当点M在什么位置时，使AM+BM的值最小？求出此时点M的坐标．
已知：点O到△ABC的两边AB、AC所在直线的距离OE、OF相等，且OB=OC．
（1）如图，若点O在边BC上，求证：AB=AC；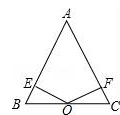
（2）如图，若点O在△ABC的内部，则（1）中的结论还成立吗？若成立，请证明；若不成立，说明理由；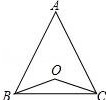
（3）若点O在△ABC的外部，则（1）的结论还成立吗？请画图表示．
在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回．设汽车从甲地出发x（h）时，汽车与甲地的距离为y（km），y与x的函数关系如图所示．根据图象信息，解答下列问题：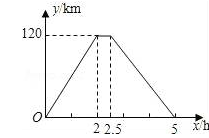
（1）这辆汽车的往、返速度是否相同？请说明理由；
（2）求返程中y与x之间的函数表达式；
（3）求这辆汽车从甲地出发4h时与甲地的距离．
给出三个多项式：
x2+x-1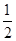，x2+3x+1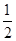，x2-x，请你写出所有其中两个多项式的加法运算，并把运算结果因式分解．
如图，在平面直角坐标系XOY中，A（-1，5），B（-1，0），C（-4，3）．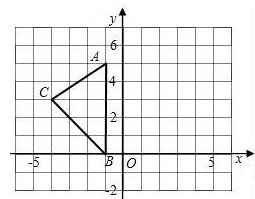
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）直接写出A′，B′，C′三点的坐标：A′（），B′（），C′（）
（3）计算△ABC的面积．