阅读感悟:
有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数 、 满足 ①, ②,求 和 的值.
本题常规思路是将①②两式联立组成方程组,解得 、 的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由① ②可得 ,由① ② 可得 .这样的解题思想就是通常所说的"整体思想".
解决问题:
(1)已知二元一次方程组 则 , ;
(2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?
(3)对于实数 、 ,定义新运算: ,其中 、 、 是常数,等式右边是通常的加法和乘法运算.已知 , ,那么 .
已知抛物线与 轴交于A(1,0),B(-3,0)两点,与
轴交于A(1,0),B(-3,0)两点,与 轴交于点C(0,3),抛物线顶点P,连接AC。
轴交于点C(0,3),抛物线顶点P,连接AC。
(1)求抛物的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与 轴交于点Q,求点D的坐标。
轴交于点Q,求点D的坐标。
(3)在抛物线的对称轴上,是否存在一点M,使得S△MAP=2S△ACP,若存在,求出M点的坐标,若不存在,请说明理由。
将一副直角三角板(Rt△ABC和Rt△DEF),按图1所示的方式摆放,∠ACB=90°,CA=CB,∠FDE=90°,O是AB中点,D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并写出证明过程。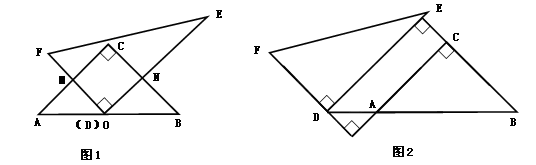
小宇同学展示出如下正确的解法:
解OM=ON,
证明:连OC,则OC是斜边AB上中线:
∵CA=CB,
∴OC是∠ACB的平分线(依据1);
∵OM⊥AC,ON⊥BC;
∴OM=ON(依据2)
(1)上述证明过程中的“依据1”“依据2”分别是指:依据1_____依据2______。
(2)你有与小宇不同的思考方法吗?请写出你的证明过程:
(3)将图(1)中的Rt△DEF沿着射线BA方向平移至图(2)所示的图形位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于N,连接OM、ON,试判断线段OM、ON的数量关系和位置关系,并写出证明过程。
如图,点P是菱形ABCD的对角线BD上的一点,连接CP并延长 ,交AD于E,交BA的延长线于F。
(1)求证:∠DCP=∠DAP.
(2)若AB=2,DP:PB=1:2,且PA⊥BF,求对角线BD的长。
关于 的一元二次方程
的一元二次方程 2+2
2+2 +
+ +1=O的实数解是
+1=O的实数解是 1和
1和 2;
2;
(1)求 的取值范围;
的取值范围;
(2)如果 1+
1+ 2-
2- 1
1 2<-1,且
2<-1,且 为整数,求
为整数,求 的值。
的值。
已知如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC,过点C作⊙O的切线,交OD的延长线于点E,连接BE:
(1)求证:BE是⊙O的切线;
(2)连接AD并延长交BE于点F,若OB=9,Sin∠ABC= ,求BF的长。
,求BF的长。