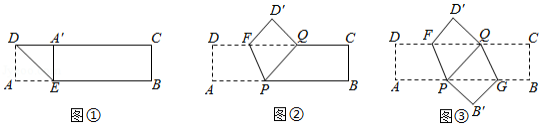
【教材呈现】如图是华师版八年级下册数学教材第121页的部分内容.
1.把一张矩形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
【问题解决】如图①,已知矩形纸片 ,将矩形纸片沿过点 的直线折叠,使点 落在边 上,点 的对应点为 ,折痕为 ,点 在 上.求证:四边形 是正方形.
【规律探索】由【问题解决】可知,图①中的△ 为等腰三角形.现将图①中的点 沿 向右平移至点 处(点 在点 的左侧),如图②,折痕为 ,点 在 上,点 在 上,那么 还是等腰三角形吗?请说明理由.
[结论应用]在图②中,当 时,将矩形纸片继续折叠如图③,使点 与点 重合,折痕为 ,点 在 上.要使四边形 为菱形,则 .

如图,在Rt△ABC中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若
在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若 ,
,
(1)求反比例函数解析式;
(2)求C点坐标.
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.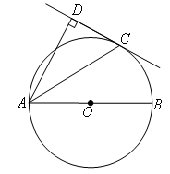
(1)求证:CD是⊙O的切线;
(2)若AC=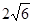 ,AD=4,求AB的长.
,AD=4,求AB的长.
在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.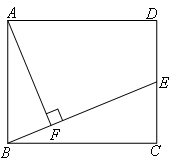
(1)求证:△BEC∽△ABF;
(2)求AF的长.
抛物线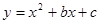 过点(2,-2)和(-1,10),与x轴交于A、B两点,与y轴交于C点.
过点(2,-2)和(-1,10),与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式.
(2)求△ABC的面积.
一次函数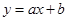 的图象与反比例函数
的图象与反比例函数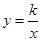 的图象交于A(1,4)、B(﹣2,m)两点,
的图象交于A(1,4)、B(﹣2,m)两点,
(1)求一次函数和反比例函数的关系式;
(2)画出草图,并根据草图直接写出不等式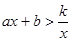 的解集.
的解集.