由于疫情的影响，学生不能返校上课，某校在直播授课的同时还为学生提供了四种辅助学习方式： 网上自测， 网上阅读， 网上答疑， 网上讨论．为了解学生对四种学习方式的喜欢情况，该校随机抽取部分学生进行问卷调查，规定被调查学生从四种方式中选择自己最喜欢的一种，根据调查结果绘制成如图两幅不完整的统计图：
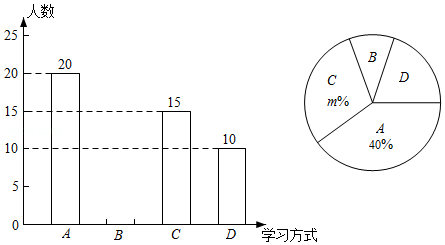
根据统计图提供的信息，解答下列问题：
（1）本次共调查了 名学生；
（2）在扇形统计图中， 的值是 ， 对应的扇形圆心角的度数是 ；
（3）请补全条形统计图；
（4）若该校共有2000名学生，根据抽样调查的结果，请你估计该校最喜欢方式 的学生人数．
如图，某中学为合理安排体育活动，在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中，随机抽取了若干名学生进行调查，了解学生最喜欢的一种球类运动，每人只能在这五种球类运动中选择一种．调查结果统计如下：
| 球类名称 |
乒乓球 |
排球 |
羽毛球 |
足球 |
篮球 |
| 人数 |
a |
12 |
36 |
18 |
b |
解答下列问题：
（1）本次调查中的样本容量是 ；
（2）a= ，b= ；
（3）试估计上述1000名学生中最喜欢羽毛球运动的人数．
如图，在平行四边形ABCD中，过AC中点O作直线，分别交AD、BC于点E、F．
求证：△AOE≌△COF．
如图，在边长为1个单位长度的小正方形组成的两格中，点A、B、C都是格点．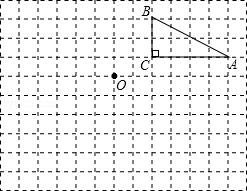
（1）将△ABC向左平移6个单位长度得到得到△A1B1C1；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．
解不等式：
，并把解集在数轴上表示出来．
（1）计算： 
（2）计算：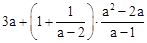
．