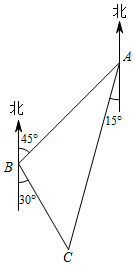
为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地 和人工智能科技馆 参观学习如图,学校在点 处, 位于学校的东北方向, 位于学校南偏东 方向, 在 的南偏西 方向 处.学生分成两组,第一组前往 地,第二组前往 地,两组同学同时从学校出发,第一组乘客车,速度是 ,第二组乘公交车,速度是 ,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号).
先化简,再求值: ,在0,1,2,三个数中选一个合适的,代入求值.
,在0,1,2,三个数中选一个合适的,代入求值.
如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
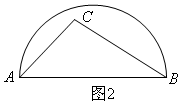
(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.
已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF。如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上。如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ。当点N到达终点B时,△GMNP和点同时停止运动。设运动时间为t秒,解答问题: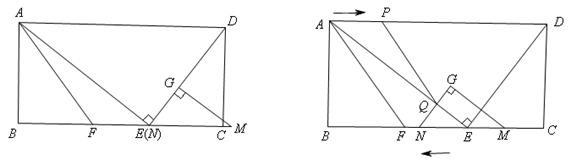
(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形,若存在,求出t的值;若不存在,说明理由;
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t的函数关系式以及自变量t的取值范围。
如图,已知抛物线 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
已知:如图,在 ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2。
ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2。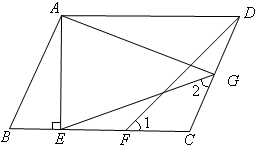
(l)若CF=2,AE=3,求BE的长;
(2)求证: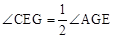 。
。