在平面直角坐标系 中,函数 和 的图象关于 轴对称,它们与直线 分别相交于点 , .
(1)如图,函数 为 ,当 时, 的长为 ;
(2)函数 为 ,当 时, 的值为 ;
(3)函数 为 ,
①当 时,求 的面积;
②若 ,函数 和 的图象与 轴正半轴分别交于点 , ,当 时,设函数 的最大值和函数 的最小值的差为 ,求 关于 的函数解析式,并直接写出自变量 的取值范围.

如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且CE=CF.
(1)求证:DF=BE;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
已知AB=AC,DB=DE,∠BAC=∠BDE=α.
(1)如图1,α=60°,探究线段CE与AD的数量关系,并加以证明;
(2)如图2,α=120°,探究线段CE与AD的数量关系,并说明理由;
(3)如图3,结合上面的活动经验探究线段CE与AD的数量关系为__________ .(直接写出答案)
探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.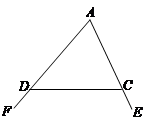
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.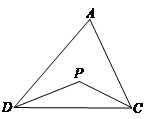
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.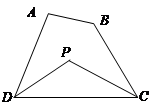
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: _______________________________.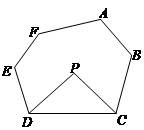
【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:AD∥BF;
(2)若AD=2,求AB的长.