【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
【探究展示】
（1）证明：AM=AD+MC；
（2）AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．
【拓展延伸】
（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．
已知圆锥的底面积和它的侧面积之比为
，求侧面展开后所得扇形的圆心角的度数。
解方程：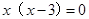
计算：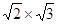
如图1, 矩形铁片ABCD中，AD="8," AB="4;" 为了要让铁片能穿过直径为3.8的圆孔, 需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).
(1)直接写出矩形铁片ABCD的面积；
(2)如图2, M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
①证明四边形MNPQ是菱形；
②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
(3)如图3, 过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合), 沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔, 并说明理由.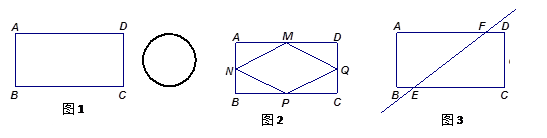
已知抛物线
过点（8，0），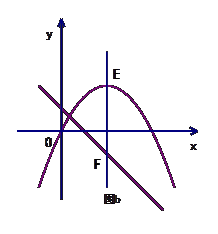
(1)求
的值；
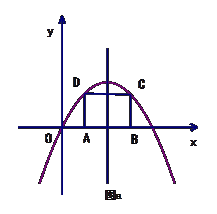
(2)如图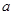
，在抛物线内作矩形ABCD，使点C、D落在抛物线上，点A、B落在
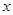轴上，设矩形ABCD的周长为L，求L的最大值；
(3)如图
，抛物线的顶点为E，对称轴与直线
交于点F．将直线EF向右平移
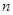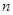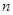个单位后（＞0），交直线于点M，交抛物线于点N，若以E、F、M、N为顶点的四边形是平行四边形，求的值．