如图,抛物线 过点 和 .点 是抛物线的顶点,点 是 轴下方抛物线上的一点,连接 , .
(1)求抛物线的解析式;
(2)如图①,当 时,求点 的坐标;
(3)如图②,在(2)的条件下,抛物线的对称轴交 轴于点 ,交线段 于点 ,点 是线段 上的动点(点 不与点 和点 重合),连接 ,将 沿 折叠,点 的对应点为点 , 与 的重叠部分为 ,在坐标平面内是否存在一点 ,使以点 , , , 为顶点的四边形是矩形?若存在,请直接写出点 的坐标,若不存在,请说明理由.

先化简,再求值: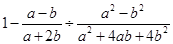 ,其中a=2,b=3.
,其中a=2,b=3.
解方程: .
.
如图,二次函数 的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).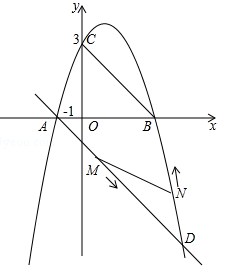
(1)求该二次函数的表达式;
(2)过点A的直线AD∥BC且交抛物线于另一点D,求直线AD的函数表达式;
(3)在(2)的条件下,请解答下列问题:①在x轴上是否存在一点P,使得以B、C、P为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由;
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动,同时,动点N以每秒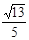 个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.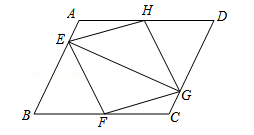
求证:(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为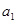 ,依次类推,排在第
,依次类推,排在第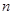 位的数称为第
位的数称为第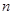 项,记为
项,记为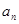 .
.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母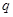 表示(
表示(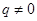 ).如:数列1,3,9,27,…为等比数列,其中
).如:数列1,3,9,27,…为等比数列,其中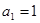 ,公比为
,公比为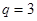 .
.
则:(1)等比数列3,6,12,…的公比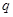 为,第4项是.
为,第4项是.
(2)如果一个数列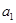 ,
, ,
,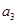 ,
,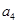 ,…是等比数列,且公比为
,…是等比数列,且公比为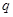 ,那么根据定义可得到:
,那么根据定义可得到: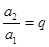 ,
, ,
,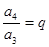 ,……
,…… 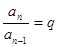 .
.
所以: ,
,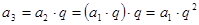 ,
,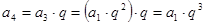 ,
,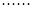
由此可得: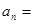 (用
(用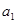 和
和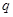 的代数式表示)
的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.