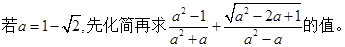有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外无其他差别,现将它们背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是奇数的概率为 .
(2)随机抽取一张卡片,然后放回洗匀,再随机抽取一张卡片,请用列表或画树状图的方法,求两次抽取的卡片上的数字和等于6的概率.
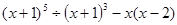
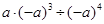
操作:如图①,点O为线段MN的中点,直线PQ与MN相交于点O,请利用图①画出一对以点O为对称中心的全等三角形。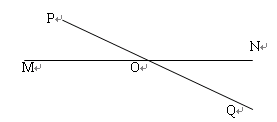
根据上述操作得到的经验完成下列探究活动:(本题12分)
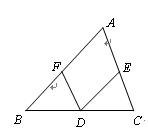
探究一:如图②,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的等量关系,并证明你的结论;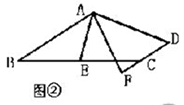
探究二:如图③,DE、BC相交于点E,BA交DE于点A,且BE:EC=1:2,∠BAE=∠EDF,CF∥AB。若AB=5,CF=1,求DF的长度。
△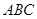 中,
中,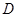 为
为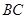 边的中点,过
边的中点,过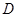 点分别作
点分别作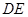 ∥
∥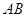 交
交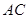 于点
于点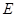 ,
,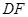 ∥
∥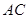 交
交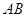 于点
于点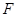 .(本题10分)
.(本题10分)
(1)证明:△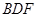 ≌△
≌△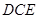 ;
;
(2)如果给△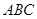 添加一个条件,使四边形
添加一个条件,使四边形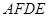 成为菱形,则该条件是;
成为菱形,则该条件是;
如果给△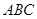 添加一个条件,使四边形
添加一个条件,使四边形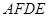 成为矩形,则该条件是.
成为矩形,则该条件是.
(均不再增添辅助线) 请选择一个结论进行证明.