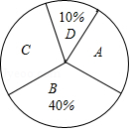
某校为了解学生课外阅读时间情况，随机抽取了 $m$ 名学生，根据平均每天课外阅读时间的长短，将他们分为 $A$ ， $B$ ， $C$ ， $D$ 四个组别，并绘制了如图不完整的频数分布表和扇形统计图．

频数分布表

组别	时间 $/$ （小时）	频 $/$ 人数
$A$	$0⩽t<0.5$	$2n$
$B$	$0⩽t<1$	20
$C$	$1⩽t<1.5$	$n+10$
$D$	$t⩾1.5$	5

请根据图表中的信息解答下列问题：

（1）求 $m$ 与 $n$ 的值，并补全扇形统计图；

（2）直接写出所抽取的 $m$ 名学生平均每天课外阅读时间的中位数落在的组别；

（3）该校现有1500名学生，请你估计该校有多少名学生平均每天课外阅读时间不少于1小时．

科目 数学   题型 解答题   难度 中等

知识点： 中位数 用样本估计总体 频数（率）分布表 扇形统计图