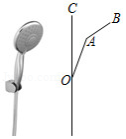
图1是挂墙式淋浴花洒的实物图,图2是抽象出来的几何图形.为使身高 的人能方便地淋浴,应当使旋转头固定在墙上的某个位置 ,花洒的最高点 与人的头顶的铅垂距离为 ,已知龙头手柄 长为 ,花洒直径 是 ,龙头手柄与墙面的较小夹角 , ,则安装时,旋转头的固定点 与地面的距离应为多少?(计算结果精确到 ,参考数据: , ,
(8分)已知图中的曲线是反比例函数y=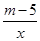 (
( 为常数)图象的一支.
为常数)图象的一支.
(1)这个反比例函数图象的另一支在第几象限?常数 的取值范围是什么?
的取值范围是什么?
(2)若该函数的图象与正比例函数y=2x的图象在第一象内限的交点为A,过A点作x轴的垂线,垂足为B,当△OAB的面积为4时,求点A的坐标及反比例函数的解析式.
(8分)如图,在4×4的正方形网格中,每个小正方形的边长都是1,△ABC三个顶点分别在正方形网格的格点上,试判断△ABC是否是直角三角形.
已知x=-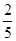 ,求
,求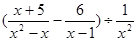 的值.
的值.
(10分) 化简:
(1)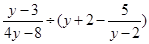 (2)计算:
(2)计算: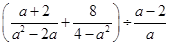
如图一,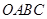 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,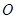 为原点,点
为原点,点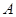 在
在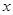 轴的正半轴上,点
轴的正半轴上,点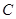 在
在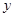 轴的正半轴上,
轴的正半轴上,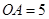 ,
,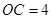 .
.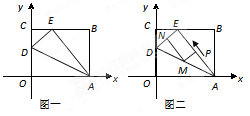
(1)在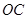 边上取一点
边上取一点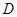 ,将纸片沿
,将纸片沿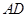 翻折,使点
翻折,使点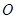 落在
落在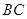 边上的点
边上的点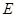 处,求
处,求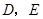 两点的坐标;
两点的坐标;
(2)如图二,若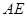 上有一动点
上有一动点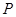 (不与
(不与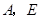 重合)自
重合)自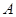 点沿
点沿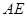 方向向
方向向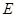 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为
点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为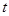 秒(
秒(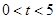 ),过
),过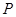 点作
点作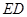 的平行线交
的平行线交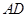 于点
于点 ,过点
,过点 作
作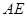 的平行线交
的平行线交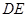 于点
于点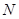 .求四边形
.求四边形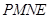 的面积
的面积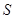 与时间
与时间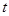 之间的函数关系式;当
之间的函数关系式;当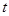 取何值时,
取何值时,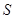 有最大值?最大值是多少?
有最大值?最大值是多少?
(3)在(2)的条件下,当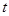 为何值时,以
为何值时,以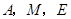 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点 的坐标.
的坐标.