已知某厂以 小时 千克的速度匀速生产某种产品(生产条件要求 ,且每小时可获得利润 元.
(1)某人将每小时获得的利润设为 元,发现 时, ,所以得出结论:每小时获得的利润,最少是180元,他是依据什么得出该结论的,用你所学数学知识帮他进行解析说明;
(2)若以生产该产品2小时获得利润1800元的速度进行生产,则1天(按8小时计算)可生产该产品多少千克;
(3)要使生产680千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
如图, 为 的直径, , 为圆上的两点, ,弦 , 相交于点 .
(1)求证: ;
(2)若 , ,求 的半径;
(3)在(2)的条件下,过点 作 的切线,交 的延长线于点 ,过点 作 交 于 , 两点(点 在线段 上),求 的长.

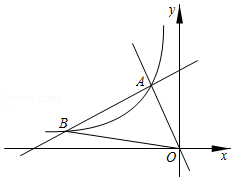
如图,在平面直角坐标系 中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.
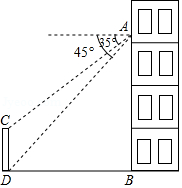
2019年,成都马拉松成为世界马拉松大满贯联盟的候选赛事,这大幅提升了成都市的国际影响力,如图,在一场马拉松比赛中,某人在大楼 处,测得起点拱门 的顶部 的俯角为 ,底部 的俯角为 ,如果 处离地面的高度 米,求起点拱门 的高度.(结果精确到1米;参考数据: , ,
随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.

根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2100人,请你估计该校对在线阅读最感兴趣的学生人数.
先化简,再求值: ,其中 .