阅读理解:
材料一:若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成"和谐三数组".
材料二:若关于 的一元二次方程 的两根分别为 , ,则有 , .
问题解决:
(1)请你写出三个能构成"和谐三数组"的实数 ;
(2)若 , 是关于 的方程 , , 均不为 的两根, 是关于 的方程 , 均不为 的解.求证: , , 可以构成"和谐三数组";
(3)若 , , 三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成"和谐三数组",求实数 的值.
某玩具商计划生产A、B两种型号的玩具投入市场,初期计划生产100件,生产投入资金不少于22400元,但不超过22500元,且资金要全部投入到生产这两种型号的玩具.假设生产的这两种型号玩具能全部售出,这两种玩具的生产成本和售价如表: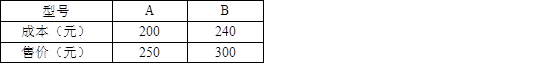
(1)该玩具商对这两种型号玩具有哪几种生产方案?
(2)该玩具商如何生产,就能获得最大利润?
如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.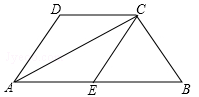
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.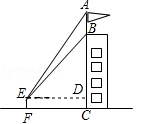
(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据: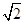 ≈1.41,
≈1.41,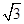 ≈1.73.
≈1.73.
先化简再求值: ,其中
,其中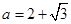 .
.
已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.