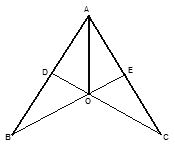
网络技术的发展对学生学习方式产生巨大的影响，某校为了解学生每周课余利用网络资源进行自主学习的时间，在本校随机抽取若干名学生进行问卷调查，现将调查结果绘制成如下不完整的统计图表，请根据图表中的信息解答下列问题
组别 |
学习时间x（h） |
频数（人数） |
A |
0＜x≤1 |
8 |
B |
1＜x≤2 |
24 |
C |
2＜x≤3 |
32 |
D |
3＜x≤4 |
n |
E |
4小时以上 |
4 |
（1）表中的n＝ ，中位数落在 组，扇形统计图中B组对应的圆心角为 °；
（2）请补全频数分布直方图；
（3）该校准备召开利用网络资源进行自主学习的交流会，计划在E组学生中随机选出两人进行经验介绍，已知E组的四名学生中，七、八年级各有1人，九年级有2人，请用画树状图法或列表法求抽取的两名学生都来自九年级的概率．
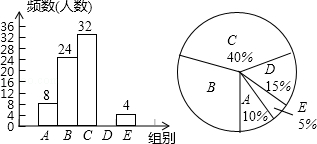
如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=500，∠C=600，求∠DAE和∠BOA的度数。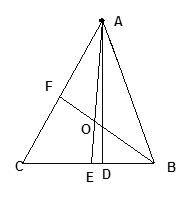
如图，已知∠A=∠D,AB="DE,AF=DC" ,请问图中有哪几对全等三角形？并任选其中一对给予证明。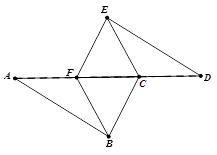
如图，△ABC中，∠B=50°，AD平分∠BAC, ∠ADC=80°，求∠C的度数。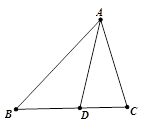
如图(1)，点A、B、C在同一直线上，且△ABE, △BCD都是等边三角形，连结AD,CE.
(1)△BEC可由△ABD顺时针旋转得到吗？若是，请描述这一旋转变换过程；若不是，请说明理由；
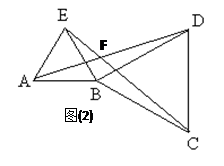
(2)若△BCD绕点B顺时针旋转，使点A,B,C不在同一直线上（如图(2)），则在旋转过程中:
①线段AD与EC的长度相等吗？请说明理由．
②锐角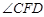
的度数是否改变？若不变，请求出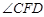的度数；若改变，请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)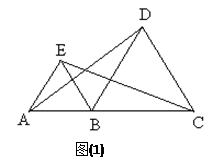
如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且AO平分∠BAC。
（1）猜想OB与OC的数量关系，并说明理由.
（2）若∠BAC=60°，问△ADC经过怎样的变换能与△AEB重合？