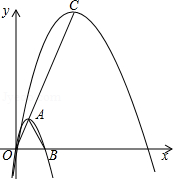
如图,抛物线
的顶点为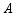 ,与
,与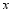 轴的正半轴交于点
轴的正半轴交于点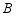 .
.
(1)将抛物线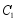 上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
(2)将抛物线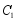 上的点
上的点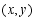 变为
变为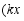 ,
,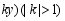 ,变换后得到的抛物线记作
,变换后得到的抛物线记作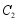 ,抛物线
,抛物线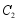 的顶点为
的顶点为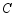 ,点
,点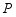 在抛物线
在抛物线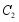 上,满足
上,满足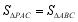 ,且
,且 .
.
①当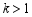 时,求
时,求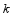 的值;
的值;
②当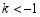 时,请直接写出
时,请直接写出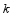 的值,不必说明理由.
的值,不必说明理由.
已知,如图,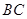 是以线段
是以线段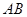 为直径的
为直径的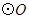 的切线,
的切线,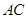 交
交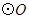 于点
于点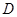 ,过点
,过点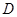 作弦
作弦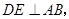 垂足为点
垂足为点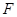 ,连接
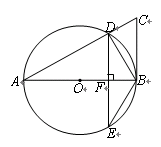
,连接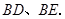 .
.
仔细观察图形并写出四个不同的正确结论:①________,②________ ,③________,④____________(不添加其它字母和辅助线,不必证明)
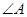 =
=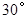 ,
,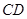 =
=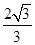 ,求
,求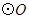 的半径
的半径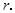
已知:关于x的方程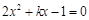
求证:方程有两个不相等的实数根
若方程的一个根是-1,求另一个根及k值
为迎接中招体育加试,需进一步了解九年级学生的身体素质,体育老师随机抽取九年级一个班共50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下图所示:
| 组别 |
次数 |
频数(人数) |
| 第1组 |
80≤x<100 |
6 |
| 第2组 |
100≤x<120 |
8 |
| 第3组 |
120≤x<140 |
12 |
| 第4组 |
140≤x<160 |
a |
| 第5组 |
160≤x<180 |
6 |
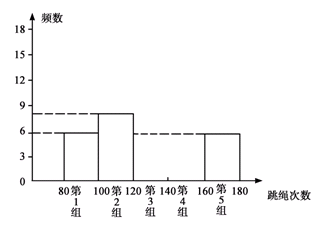
请根据图表信息完成下列问题直接写出表中a的值;
请把频数分布直方图补充完整;
若在一分钟内跳绳次数少于120次的为测试不合格,则该班学生进行一分钟跳绳不合格的概率是多少?
超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为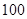 米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为
米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为 秒且∠APO=60°,∠BPO =45°.
秒且∠APO=60°,∠BPO =45°. 
求A、B之间的路程
请判断此出租车是否超过了城南大道每小时60千米的限制速度?
(参考数据: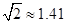 ,
,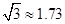 )
)
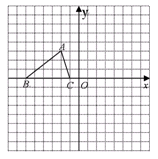
如图,已知 的三个顶点的坐标分别为
的三个顶点的坐标分别为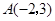 、
、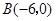 、
、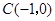 .
.
请直接写出点
 关于
关于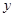 轴对称的点的坐标
轴对称的点的坐标将
 绕坐标原点
绕坐标原点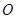 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点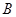 的对应点的坐标
的对应点的坐标请直接写出:以
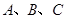 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点 的坐标.
的坐标.