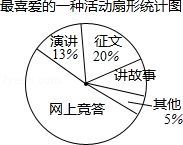
近期，我市中小学广泛开展了“传承中华文化，共筑精神家园”爱国主义读书教育活动，某中学为了解学生最喜爱的活动形式，以“我最喜爱的一种活动”为主题，进行随机抽样调查，收集数据整理后，绘制出以下两幅不完整的统计图表，请根据图中提供的信息，解答下面的问题：
最喜爱的一种活动统计表
活动形式 |
征文 |
讲故事 |
演讲 |
网上竞答 |
其他 |
人数 |
60 |
30 |
39 |
|
|
（1）在这次抽样调查中，一共调查了多少名学生？扇形统计图中“讲故事”部分的圆心角是多少度？
（2）如果这所中学共有学生3800名，那么请你估计最喜爱征文活动的学生人数．
（本题满分12分，每小题满分各6分）
已知：直角坐标系xoy中，将直线
沿y轴向下平移3个单位长度后恰好经过B(-3，0)及y轴上的C点．若抛物线
与
轴交于A，B两点（点A在点B的右侧），且经过点C，（1）求直线
及抛物线的解析式；（2）设抛物线的顶点为
，点
在抛物线的对称轴上，且
，求点的坐标；
(本题14分)如图，在平面直角坐标系中，抛物线
与x轴交于A、B两点(A点在B点左侧)，与y轴交于C点，顶点为D.过点C、D的直线与x轴交于E点，以OE为直径画⊙O1，交直线CD于P、E两点.
(1)求E点的坐标；
(2)联结PO1、PA.求证:
～
；
(3) ①以点O2 (0，m)为圆心画⊙O2，使得⊙O2与⊙O1相切，当⊙O2经过点C时，求实数m
的值；
②在①的情形下，试在坐标轴上找一点O3，以O3为圆心画⊙O3，使得⊙O3与⊙O1、⊙O2同时相切.直接写出满足条件的点O3的坐标(不需写出计算过程).
(本题12分)
如图，AD//BC，点E、F在BC上，∠1=∠2，AF⊥DE，垂足为点O.
(1
)求证:四边形AEFD是菱形；
(2)若BE=EF=FC，求∠BAD+∠ADC的度数；
(3)若BE=EF=FC，设AB = m，CD = n，求四边形ABCD的面积.
(本题12分)如图，在平面直角坐标系中，等腰梯形OABC，CB//OA，且点A在x轴正半轴上.已知C(2，4)，BC= 4.
(1)求过O、C、B三点的抛物线解析式，并写出顶点坐标和对称轴；
(2)经过O、C、B三点的抛物线上是否存在P点(与原点O不重合)，使得P点到两坐标轴的
距离相等.如果存在，求出P点坐标；如果不存在，请说明理由.
22(本题10分)为缓解交通压
力，节约能源减少大气污染，上海市政府推行“P+R”模式(即:开自驾车人士，将车开到城郊结合部的轨道车站附近停车，转乘轨道交通到市中心).市郊某地正在修建地铁站，拟同步修建地下停车库.
(提供可选用的数据:
)
