阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题是，有如下思路：连接AC．
结合小敏的思路作答
（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决以下问题：
（2）如图2，在（1）的条件下，若连接AC，BD．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．
如图，矩形ABCD中，点O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO．若∠COB=60°，FO=FC．
求证：（1）四边形EBFD是菱形； （2）MB : OE=3：2 ．
一次函数
的图象经过A（0，﹣2），B（1，0）两点，与反比例函数
的图象在第一象限内的交点为M（m，4）．
（1）求一次函数和反比例函数的表达式；
（2）在x轴上是否存在点P，使AM⊥MP？若存在，求出点P的坐标；若不存在，说明理由．
A，B两个火车站相距360km．一列快车与一列普通列车分别从A，B两站同时出发相向而行，快车的速度比普通列车的速度快54km/h，当快车到达B站时，普通列车距离A站还有135km．求快车和普通列车的速度各是多少？
已知关于x的方程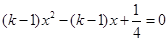
有两个相等的实数根，求实数k的值．
若实数a满足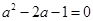
，计算
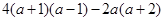的值．