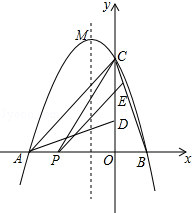
如图，二次函数y＝ax2+bx+c的图象交x轴于A、B两点，交y轴于点C，且B（1，0），C（0，3），将△BOC绕点O按逆时针方向旋转90°，C点恰好与A重合．
（1）求该二次函数的解析式；
（2）若点P为线段AB上的任一动点，过点P作PE∥AC，交BC于点E，连结CP，求△PCE面积S的最大值；
（3）设抛物线的顶点为M，Q为它的图象上的任一动点，若△OMQ为以OM为底的等腰三角形，求Q点的坐标．
如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件，请你在其中选3个作为条件，余下的1个作为结论，使其成为一个真命题，并加以证明。（1）BE=CF，（2）AC = DF，（3）∠ABC=∠DEF，（4）AB=DE．
我所选择的真命题是：
如图，已知：
求证：
证明：
解方程：
(1)计算与化简：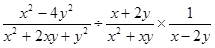
（2）解不等式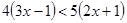
并把它的解集在数轴上表示出来
为迎接旅游节，某宾馆将总面积为6000平方米的房屋装修改造成普通客房（每间26平方米）和高级客房（每间36平方米）共100间及其他功能用房若干间，要求客房面积不低于总面积的50%，又不超过总面积的60%
（1）求最多能改造成普通客房多少间
（2）在（1）的情况下，旅游节期间，普通客房以每间每天100元的价格全部租出，高级客房每天租出的间数y（间）与其价格x（元/间）之间的关系如图所示试问：该宾馆一天的最高客房收入能达到12000元吗？若能，求出此时高级客房的价格；若不能，请说明理由
如图，在平面直角坐标系xOy中，直线
与x轴，y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处
（1）求AB的长和点C的坐标；
（2）求直线CD的解析式