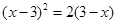某射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了8次测试，测试成绩（单位：环）如下表：
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
第七次 |
第八次 |
|
甲 |
10 |
8 |
9 |
8 |
10 |
9 |
10 |
8 |
乙 |
10 |
7 |
10 |
10 |
9 |
8 |
8 |
10 |
（1）根据表格中的数据，计算出甲的平均成绩是 环，乙的平均成绩是 环；
（2）分别计算甲、乙两名运动员8次测试成绩的方差；
（3）根据（1）（2）计算的结果，你认为推荐谁参加全国比赛更合适，并说明理由．
某种商品，按标价销售每件可盈利50元，平均每天销售24件，根据市场信息，若每件降价2元，则每天可多销售6件，如果经销商想保证每天盈利2160元，同时考虑不过多增加营业员的工作量，即每天销售不超过100件，每件商品应降价多少元？
为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图（如图），图中从左到右依次为第1、2、3、4、5组。
（1）求抽取了多少名学生参加测试？
（2）处于哪个次数段的学生数最多？
（答出是第几组即可）
（3）若次数在5次（含5次）以上为达标，
求这次测试的达标率。
如右图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求
（1）△ABC的面积；
（2）△ABC的周长；
（3）点C到AB边的距离．
(6分)如图，某水坝的横断面是梯形，坝顶宽8米，坝高20米，斜坡AD的坡比为
，斜坡BC的坡比为
，求坝底AB的长.
用适当的方法解方程：
（1）
（2）
（3） 
（4）