如右图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求
(1)△ABC的面积;
(2)△ABC的周长;
(3)点C到AB边的距离.
如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为12米时,球移动的水平距离PD为9米 .已知山坡PA与水平方向PC的夹角为30o,AC⊥PC于点C, P、A两点相距 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 
(1)求水平距离PC的长;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从P点直接打入球洞A.
阅读下面材料:
小伟遇到这样一个问题:如图1,在正三角形ABC内有一点P,且PA="3" ,PB=4,PC=5,求∠APB的度数.
小伟是这样思考的:如图2,利用旋转和全等的知识构造△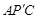 ,连接
,连接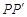 ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.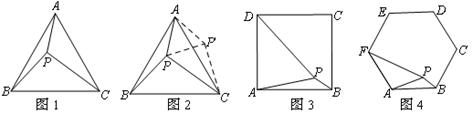
请你回答:图1中∠APB的度数等于 .
参考小伟同学思考问题的方法,解决下列问题:
(1)如图3,在正方形ABCD内有一点P,且PA= ,PB=1,PD=
,PB=1,PD=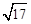 ,则∠APB的度数等于,正方形的边长为;
,则∠APB的度数等于,正方形的边长为;
(2)如图4,在正六边形ABCDEF内有一点P,且PA=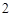 ,PB=1,PF=
,PB=1,PF= ,则∠APB的度数等于,正六边形的边长为.
,则∠APB的度数等于,正六边形的边长为.
在矩形ABCD中,点O在对角线BD上,以OD为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.
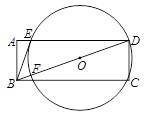
(1)求证:BE与⊙O相切;
(2)若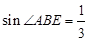 ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
如图,在Rt△ABC中,∠CAB=90°,AD是∠CAB的平分线,tanB=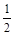 ,求
,求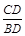 的值.
的值.
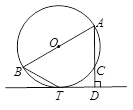
如图,AB为⊙O的直径,直线DT切⊙O于T,AD⊥DT于D,交⊙O于点C,AC=2,DT =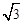 ,求∠ABT的度数.
,求∠ABT的度数.