如图所示,抛物线 y= ax 2﹣  x+ c经过原点 O与点 A(6,0)两点,过点 A作 AC⊥ x轴,交直线 y=2 x﹣2于点 C,且直线 y=2 x﹣2与 x轴交于点 D.
x+ c经过原点 O与点 A(6,0)两点,过点 A作 AC⊥ x轴,交直线 y=2 x﹣2于点 C,且直线 y=2 x﹣2与 x轴交于点 D.
(1)求抛物线的解析式,并求出点 C和点 D的坐标;
(2)求点 A关于直线 y=2 x﹣2的对称点 A′的坐标,并判断点 A′是否在抛物线上,并说明理由;
(3)点 P( x, y)是抛物线上一动点,过点 P作 y轴的平行线,交线段 CA′于点 Q,设线段 PQ的长为 l,求 l与 x的函数关系式及 l的最大值.

如下图所示,在△ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.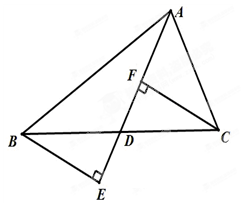
先化简,再求值: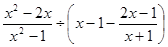 ,选一个你喜欢的实数x代入求值.
,选一个你喜欢的实数x代入求值.
(本题14分)阅读:在用尺规作线段 等于线段
等于线段 时,小明的具体做法如下:
时,小明的具体做法如下: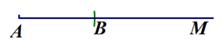
已知:如图,线段 .
.
求作:线段 ,使得线段
,使得线段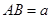 .
.
作法: ① 作射线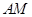 ;
;
② 在射线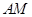 上截取
上截取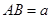 .
.
∴线段 为所求.
为所求.
解决下列问题:已知:如图,线段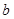 .
.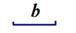
(1)请你仿照小明的作法,在上图中的射线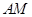 上作线段
上作线段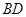 ,使得
,使得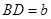 ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取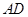 的中点
的中点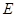 .若
.若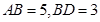 .
.
①当点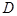 在线段
在线段 上时(画出图形)。段
上时(画出图形)。段 的长.
的长.
②当点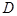 在线段
在线段 的延长线上时(画出图形). 求线段
的延长线上时(画出图形). 求线段 的长.
的长.
(本题12分)魔术师为大家表演魔术. 他请观众想一个数,然后将这个数按以下步骤操作:
魔术师立刻说出观众想的那个数.
(1)如果小明想的数是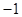 ,那么他告诉魔术师的结果应该是;
,那么他告诉魔术师的结果应该是;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,我们发现假设想的数为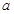 时,请按魔术师要求的运算过程写成代数式?
时,请按魔术师要求的运算过程写成代数式?
(4)化简(3)所列的代数式并化简,请你用一句话说出其中的奥妙.
(本题10分)在“读书月”活动中,学校把一些图书分给某班学生阅读,若每个人分3本,则剩余20本;若每个人分4本,则还缺少25本.这个班有多少名学生?