如图,在△ ABC中,∠ C=90°, D、 F是 AB边上两点,以 DF为直径的⊙ O与 BC相交于点 E,连接 EF,∠ OFE= ∠ A.过点 F作 FG⊥ BC于点 G,交⊙ O于点 H,连接 EH.
(1)求证: BC是⊙ O的切线;
(2)连接 ED,过点 E作 EQ⊥ AB,垂足为 Q,△ EQD和△ EGH全等吗?若全等,请予以证明;若不全等,请说明理由;
(3)当 BO=5, BE=4时,求△ EHG的面积.

如图(1),AB、BC、CD分别与⊙O相切于点E、F、G,且AB∥CD,若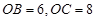 ,
,
求BC和OF的长;
求证:
 三点共线;
三点共线;小叶从第(1)小题的计算中发现:等式
 成立,于是她得到这样的结论:如图(2),在
成立,于是她得到这样的结论:如图(2),在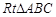 中,
中,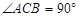 ,
,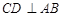 ,垂足为
,垂足为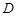 ,设
,设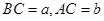 ,
, ,则有等式
,则有等式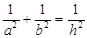 成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.
成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.
如图,直线l经过点A(1,0),且与曲线 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线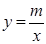 (x>0)和
(x>0)和 (x<0)于M,N两点.
(x<0)于M,N两点.
求m的值及直线l的解析式;
是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由
某班将开展“阳光体育”活动,班长在班里募捐了80元给体育委员小明去购买体育用品.小明买了5个毽子和8根跳绳,毽子每个2元,共花了34元.买回后班长觉得用品不够,还需再次购买,下面两图是小明再次买回用品时与班长的对话情境,请根据所给的信息,解决问题:
试计算每根跳绳多少元?
试计算第二次买了毽子和跳绳各多少件?
请你解释:为什么不可能找回33元?
如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.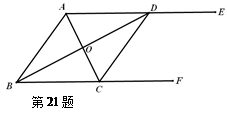
求证:△AOD≌△COB
求证:四边形ABCD是菱形.
如图, 的三个顶点都在
的三个顶点都在 的网格(每个小正方形的边长均为1个单位长度)的格点上.
的网格(每个小正方形的边长均为1个单位长度)的格点上.
在网格中画出将
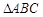 绕点B顺时针旋转90°后的
绕点B顺时针旋转90°后的
△A′BC′的图形.求点
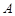 在旋转中经过的路线的长度.(结果保留
在旋转中经过的路线的长度.(结果保留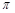 )
)